Games101笔记 P11~?
贝塞尔曲线(Bezier Curve-General Algebraic Formula)
三个点的贝塞尔曲线迭代公式:
\[b^1_0(t)=(1-t)b_0+tb_1 \]
\[b_1^1(t)=(1-t)b_1+tb_2 \]
\[b_0^2(t)=(1-t)b_0^1+tb_!^1 \]
展开得到
\[b^2_0(t)=(1-t)^2b_0+(1-t)tb_1+t^2b_2 \]
n个控制点的贝塞尔曲线,每一个时刻曲线上的点的坐标,可以通过二项式展开得到。
\[b^n(t)=b_0^n(t)=\sum^n_{j=0}b_j B^n_j(t) \]
其中\(B^n_j(t)\)就是伯恩斯坦多项式,也就是二项式展开的系数,写作:
\[B_i^n(t)=(n,i)^Tt^i(1-t)^{n-1}={C_n^i}t^i(1-t)^{n-i} \]
用语言表述就是,用伯恩斯坦系数给各个控制点加权得到贝塞尔曲线的解。
优美的性质->1.线性不变:贝塞尔曲线只需要记录控制点的位置,在线性变换下,对控制点进行变换之后重新生成的曲线与直接对曲线进行变换得到的曲线相同。
2.凸包性:贝塞尔曲线一定在控制点形成的凸包内。
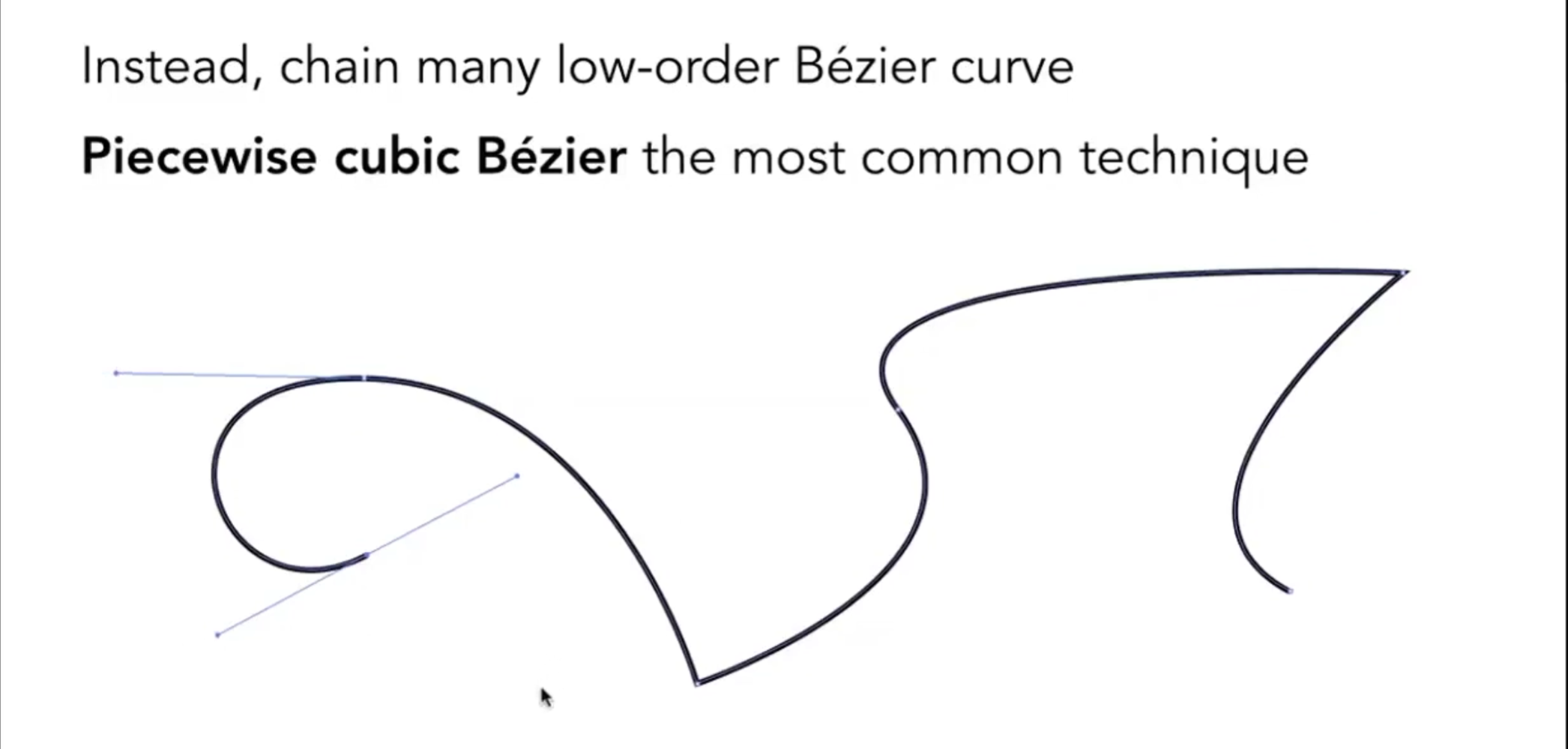
逐段的贝塞尔曲线
因为在控制点很多的时候,每一个控制点对曲线的影响很小了,人们更趋向于使用较少的控制点和较多的贝塞尔曲线,来刻画曲线,一般使用四个控制点来处理一段曲线,然后把各段曲线连起来,可以得到不错的效果。
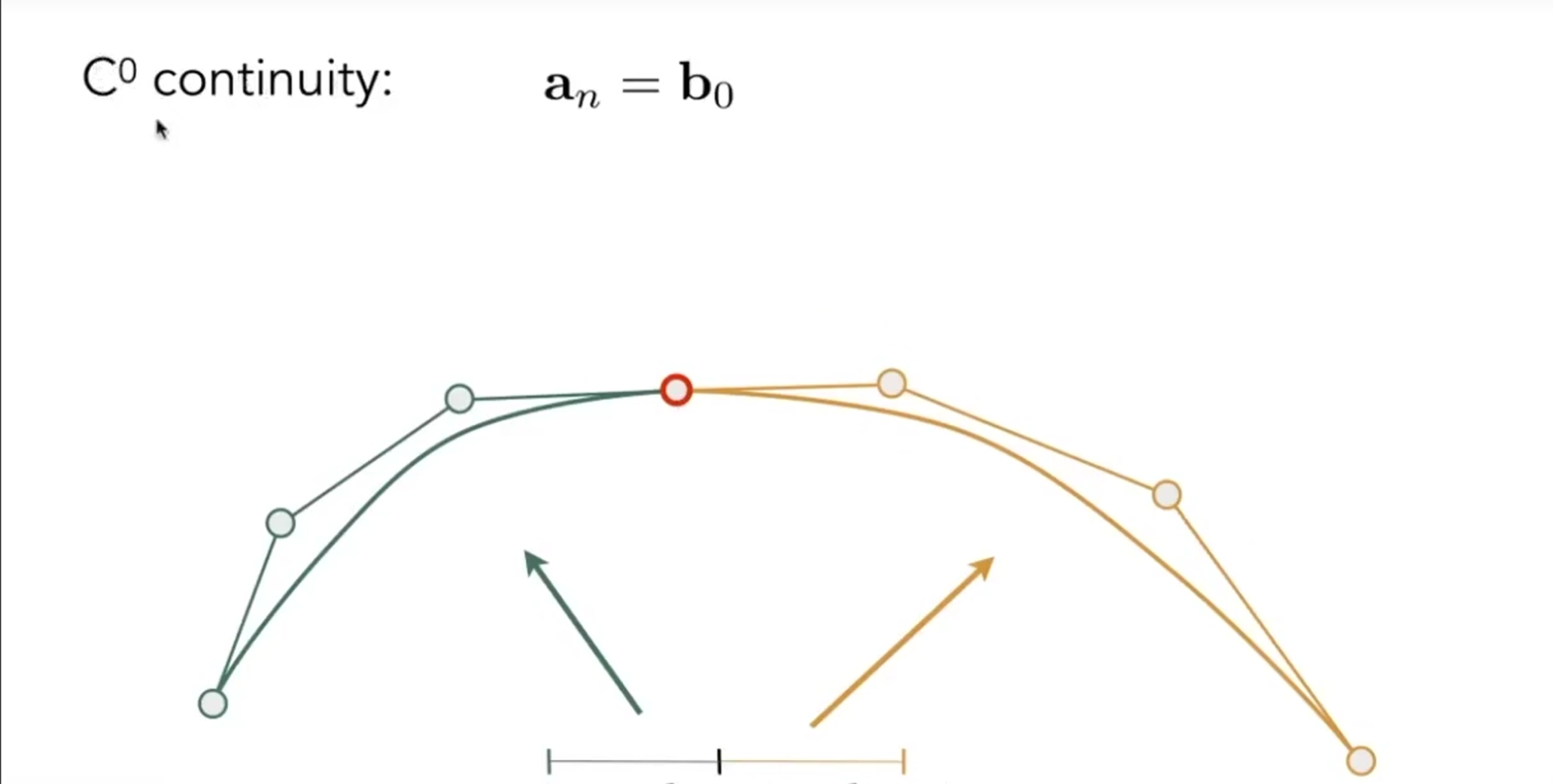
当一条贝塞尔的曲线的终点和另一条贝塞尔曲线的起点重合时即\(a_n=b_0\),我们叫它\(C_0\)连续。也就是函数连续。
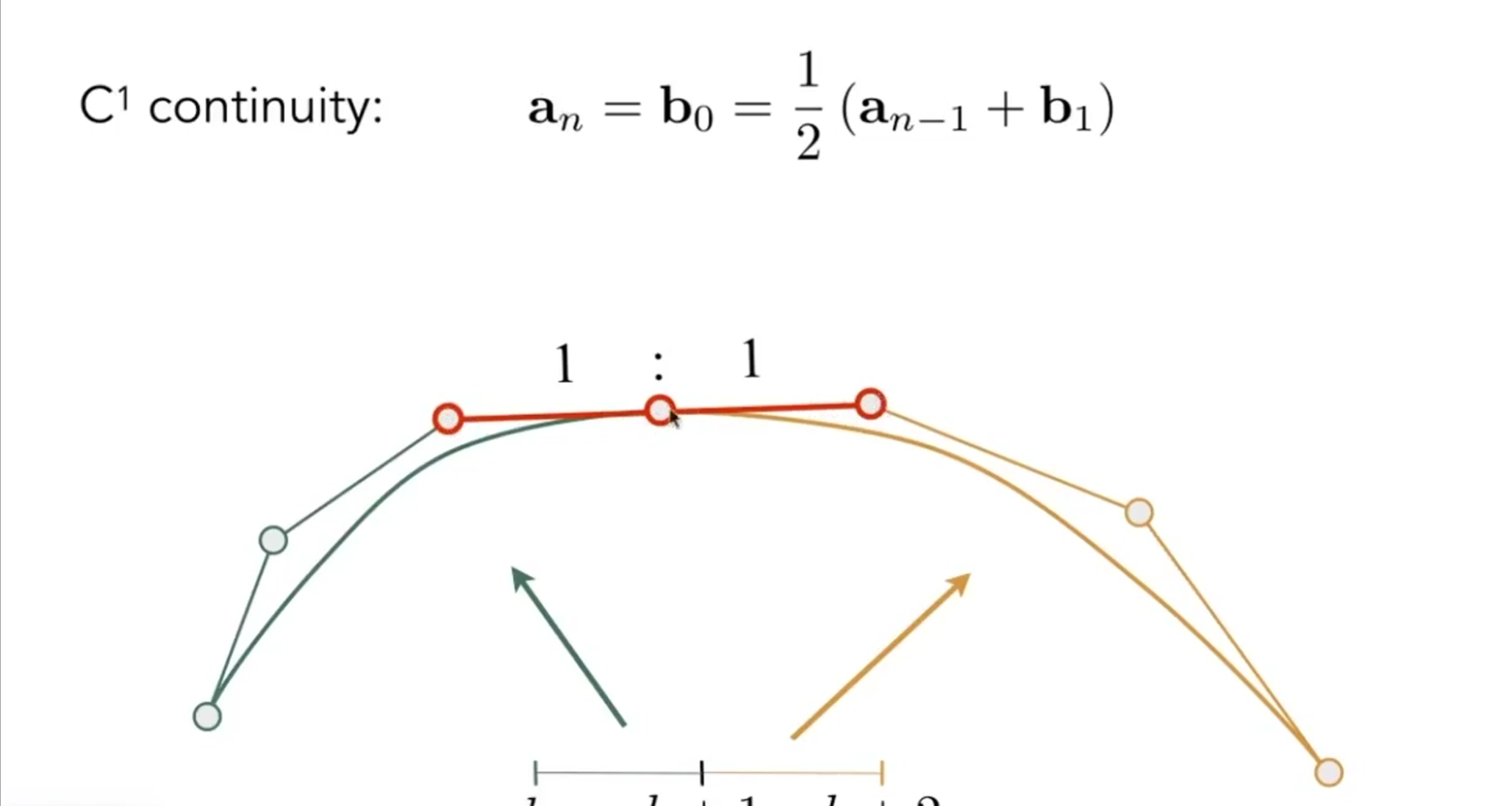
在\(C_0\)连续的情况下,当一条贝塞尔曲线的终止向量的和另一个贝塞尔曲线的起始向量反向相等时,我们称之为\(C_1\)连续。理解起来就是这条曲线在这点导数连续。
Bezier Surfaces(贝塞尔曲面)
用四条贝塞尔曲线的点当作四个控制点,再生成一条贝塞尔曲线,然后遍历之前的贝塞尔曲线,就可以得到贝塞尔曲面。
如图,四个贝塞尔曲线上的点形成了新的控制点,然后绘制新的贝塞尔曲线。
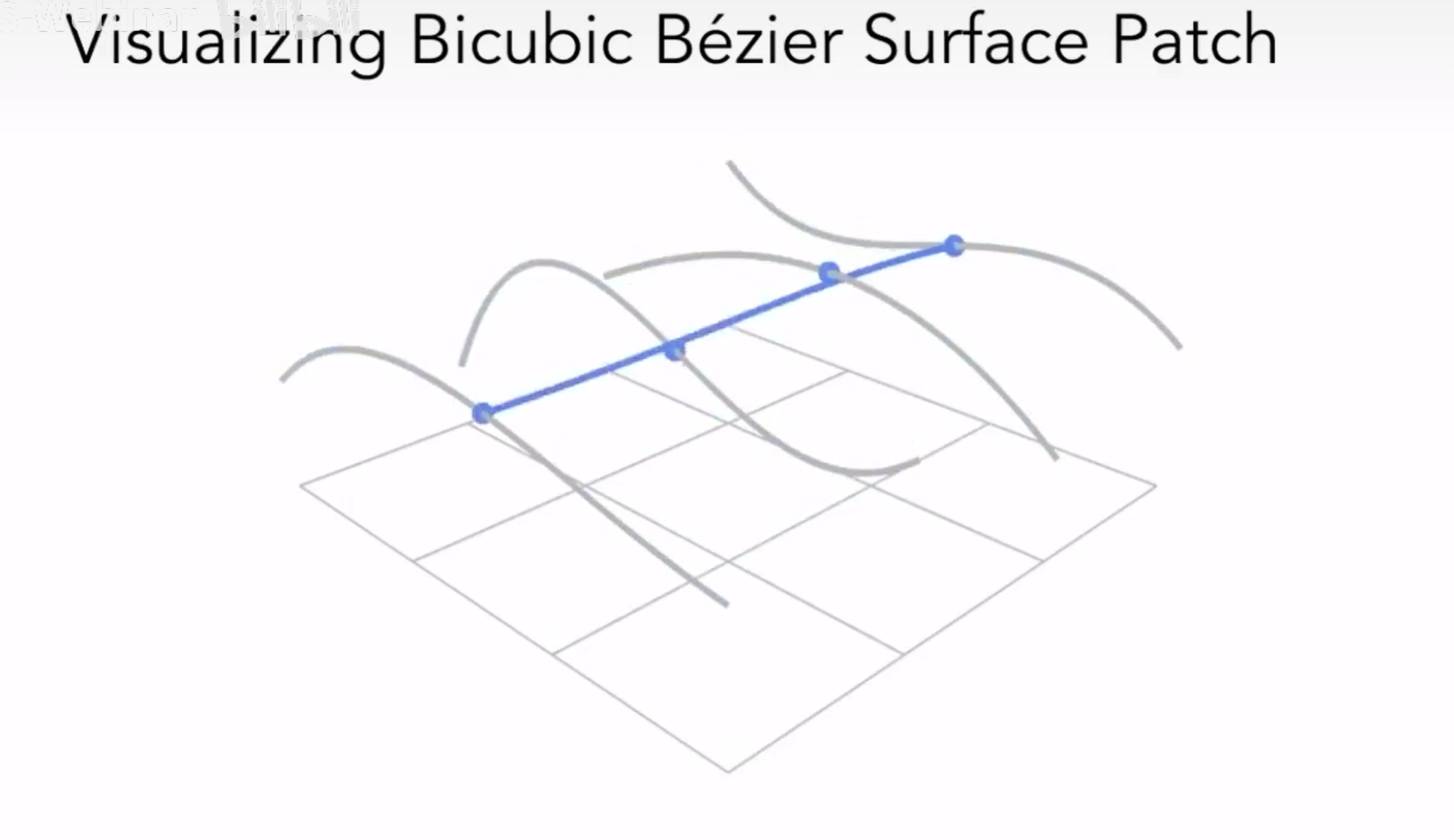
最后形成贝塞尔曲面:

网格细分(Mesh Subdivision)
一、Loop Subdivision(发明人叫Loop和循环没关系)
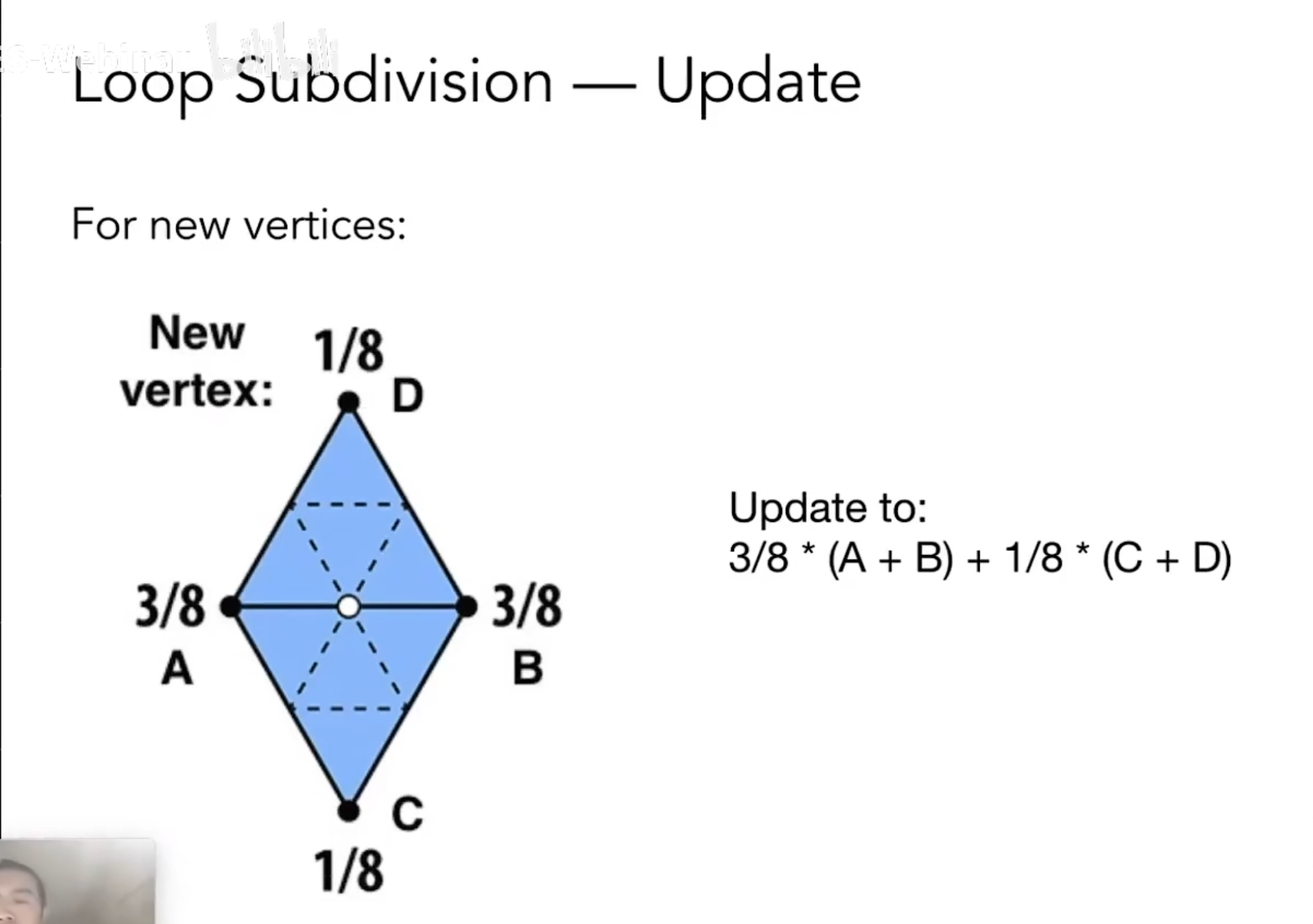
对新顶点
通过提高三角形的数量来提高模型的质量,把一个三角形分成等大的四块三角形。对于一般情况添加的点来说它会由两三角形所共享,那么这个点就可以由已知的两个三角形所确定。具体就是取加权平均数。
\[E=\frac{3}{8}(A++B)+\frac{1}{8}(C+D) \]
其中E点就在AB线段上,C、D就是两个三角形的另外两个顶点。
对旧的顶点
对于旧的顶点,参考周围的老的顶点,按照“度”(就是一个节点与周围的连线的数量)来进行加权平均,当然旧的点也需要参考自己的坐标。
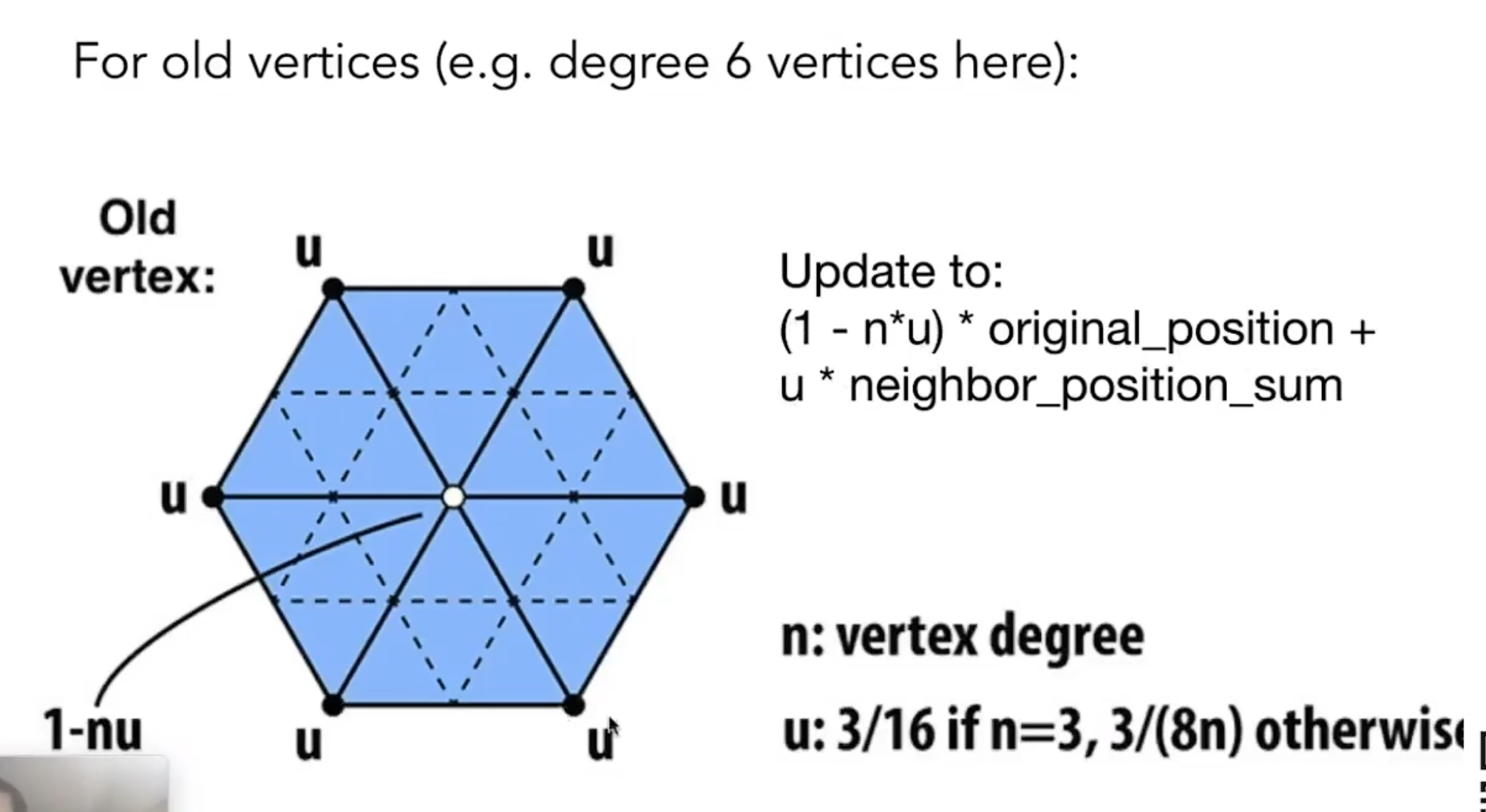
其中 u 就是旧节点的度,这里是6。u 就是需要周围点的权值,参考度来生成。除去周围节点的权值,剩下的就是旧节点自己所占的权值了。
二、Catmull-Clark Subdivision(General Mesh)
Loop Subdivision只能处理三角形网格,Catmull则可以细分四边形网格。
定义
Non-quad face——非四边形面
Extrordinary vertex(degree!=4)——奇异点(度不等于4的点)

操作
在每一条边上取中电,每一个面上取中点,然后把这些点连起来,增加面密度。
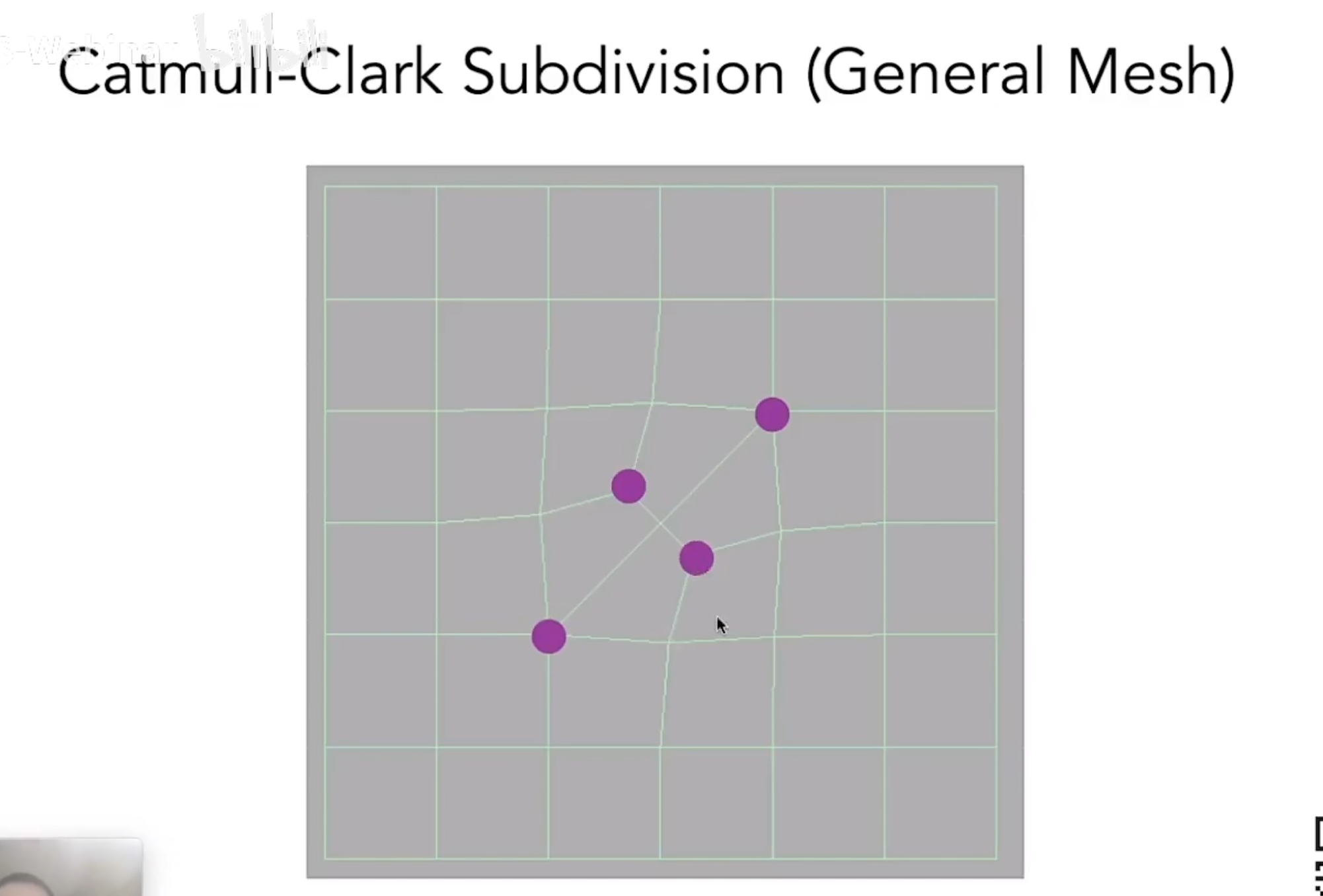
经过一次操作,把所有的非四边形面变成了奇异点,使得所有的面都是四边形面,又因为非四边形面细分之后得到奇异点,所以在第一次细分之后不会再出现非四边形面。
点的更新
第一类:四边形中间的点(Face Point)
直接取顶点的平均即可
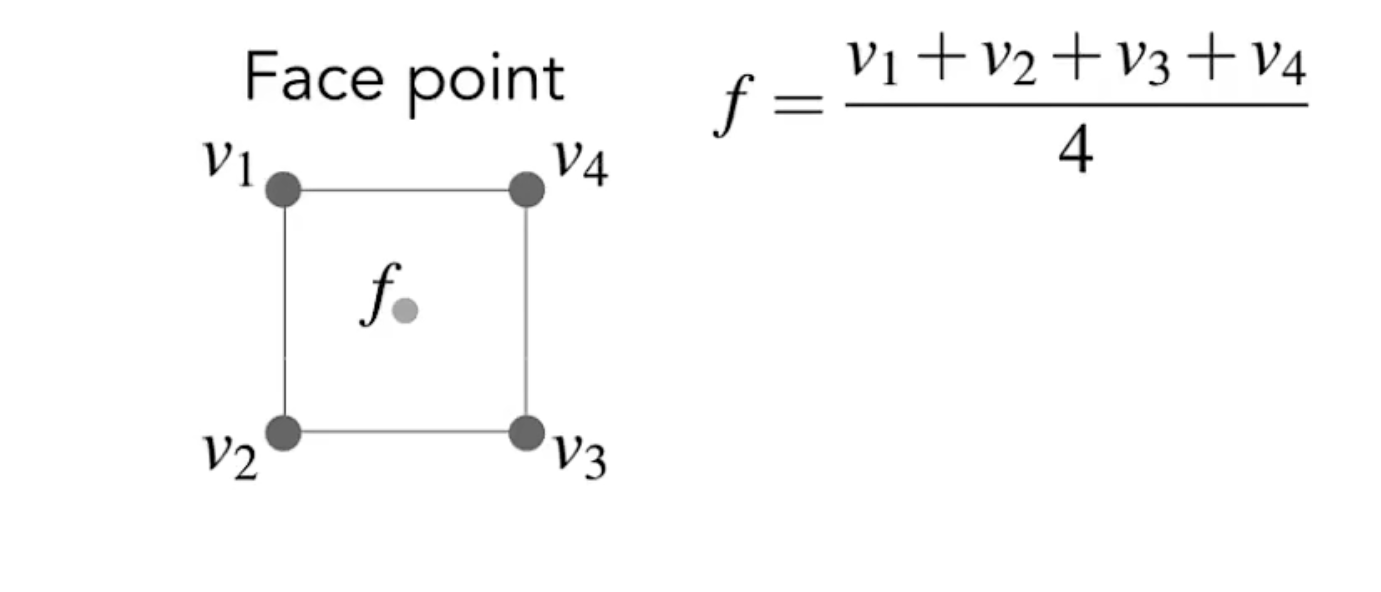
第二类:在边上的点(Edge Point)
参照构成该边的两个点和附近两个区域的内点进行平均(无视图中的f )
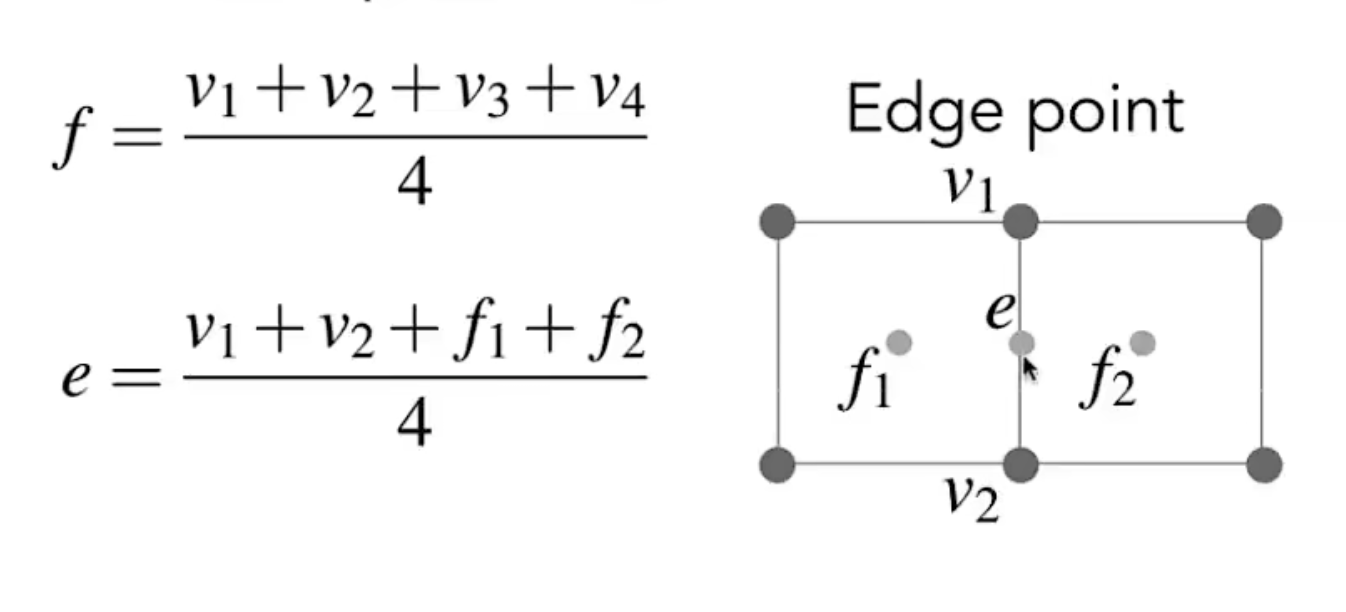
第三类:顶点(Vertex Point)
使用周围的八个点和自身,进行加权平均计算
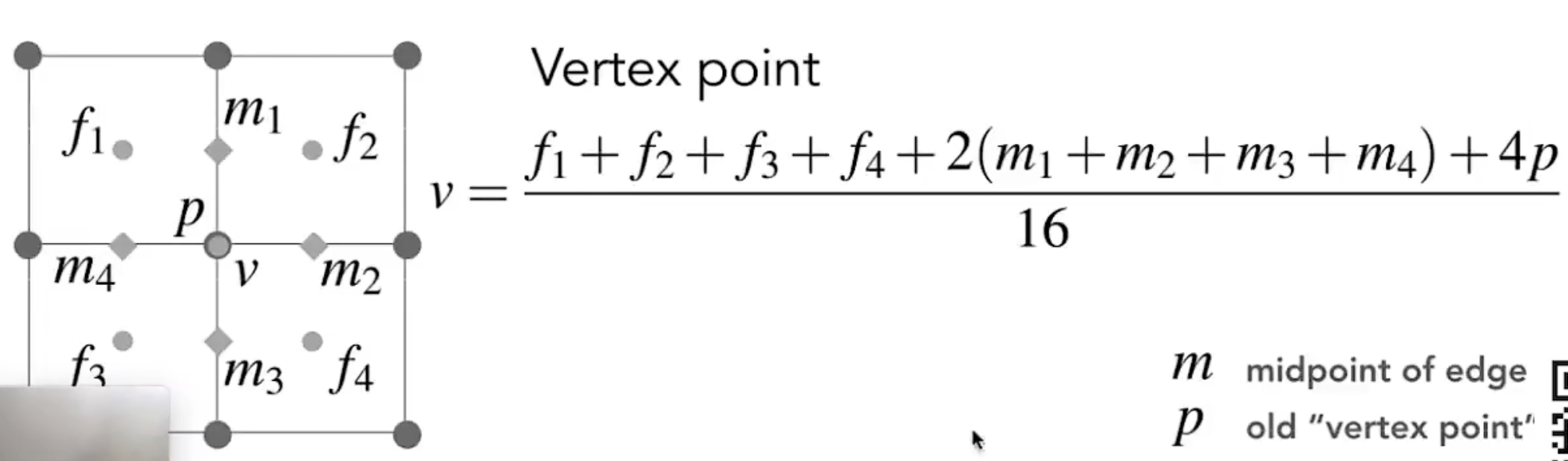
网格简化(Mesh Simplification)
目的
Goal : reduce number of mesh elements while maintaining the overall shape.
在保证模型不走样的情况下,减少网格元素。
edge collapsing 边塌缩
边塌缩不是随便删除点就行,需要进行二次度量误差Quadric Error Metrics
Quadric Error Of Edge Collapse 二次度量误差
计算二次度量误差,给每一个边进行二次度量误差检查,给每一个边进行计算,得到一个二次度量误差。从二次度量误差最小的开始。然后每次塌缩最小的一条边,再更新被影响的边。
Shadows(阴影)
Shadow Mapping
只能处理点光源
Key idea 中心思想
如果一个点不在阴影里面,那么这个点可以被光源看到,也可以被相机看到。
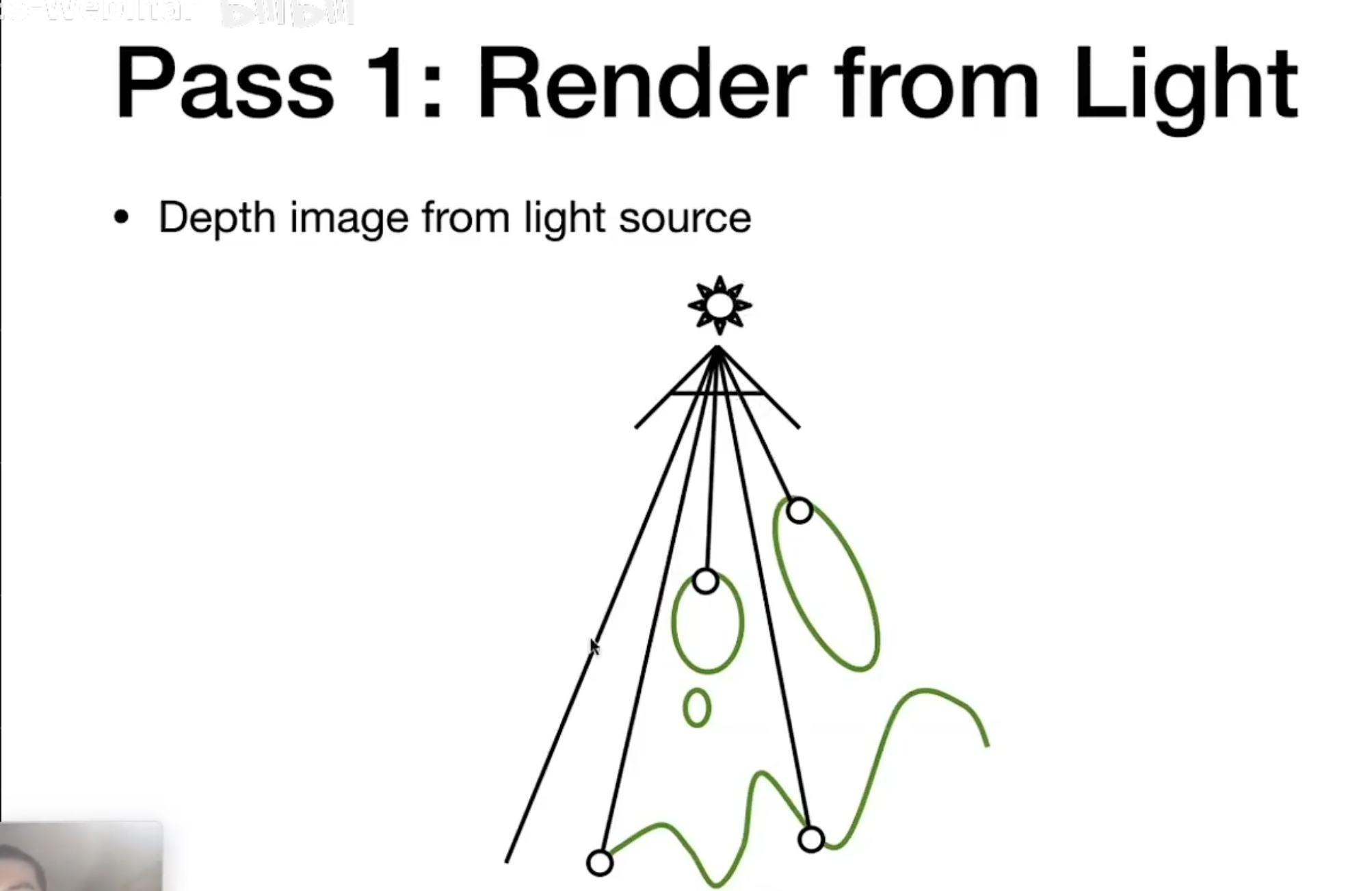
Pass1 :Render from Light 从光源进行光栅化
>Depth image from light sourse 从光源进行光栅化,记录点的深度
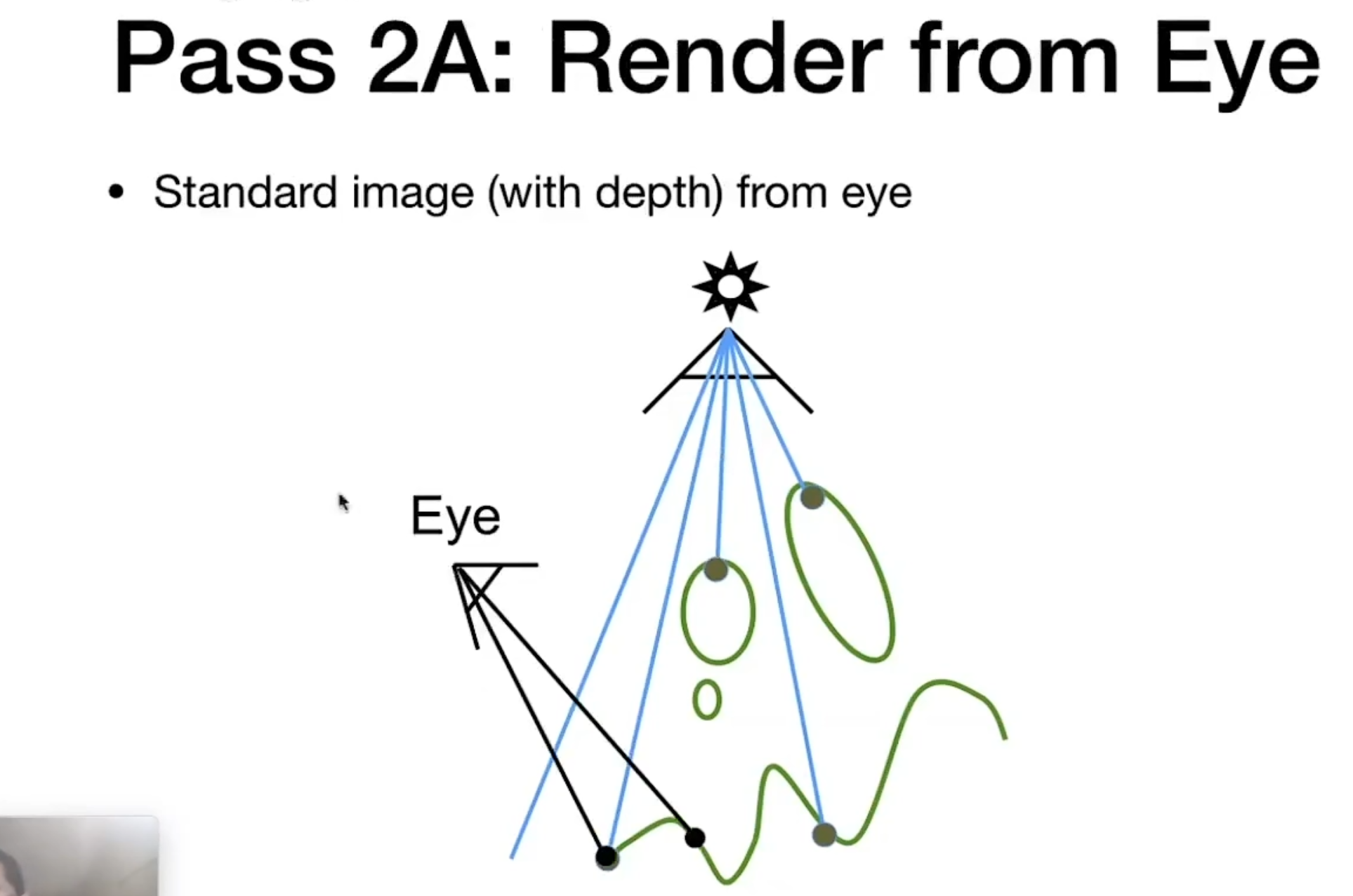
Pass2A:Render from eye
从摄像机进行光栅化
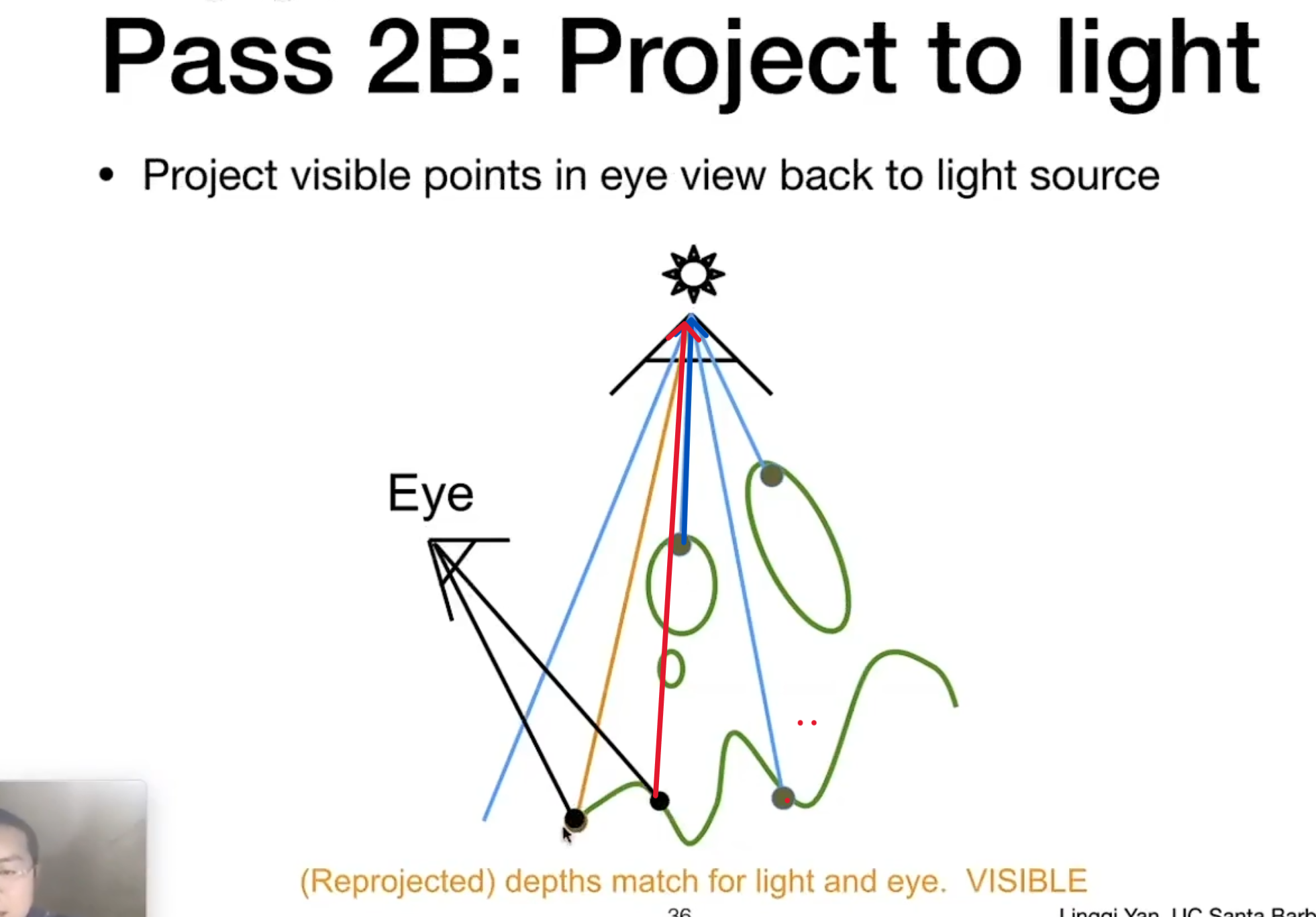
Pass2B:Project to light
把摄像机中的点和这个点对于光源的深度和之前光源光栅化记录的深度进行比较,如果深度一样,说明这个点是可见的,可以被光源和摄像机同时看到。但是如果深度不一样,如图红色的深度是对于光源的深度,蓝色的深度是记录的深度,但深度大于记录的深度时,说明这个点无法被光照到。
Problems with shadow maps
shadow maps只能做硬阴影,也就是说阴影要么是黑,要么是白,但是现实生活中是软阴影,因为非点光源导致的影子是存在本影和伴影,所以Shadow maps 只能做点光源的阴影,但是不能做立体光源的阴影,也就是软阴影。

Ray Tracing 光线追踪
Why Ray Tracing?
Rasterization could’t handle global effects well
光栅化不能很好的表现全局的效果
And especially when the light bounces more than once
光栅化无法很好的处理光线在场景中反射了不止一次的情况
(Soft)shadows 不能很好的表示和软阴影
Glossy reflection 光泽反射
indirect illumination 间接光照

光栅化在处理多次反射的时候会比较麻烦,而且不能保证物理上的正确性。相当于光珊化是一种快速的近似。而光线追踪是非常非常慢的,很真实的图形,一般用于离线,比如动画的渲染。
Basic Ray-Tracing Algorithm
Light Rays 光线
Three ideas about light rays
1.Light travels in straight lines 光线沿直线传播
2.Light rays do not “collide” with each other if they cross 光路互不干扰
(though are wrong)
3.Light rays travel from the light sources to the eye(光路可逆)
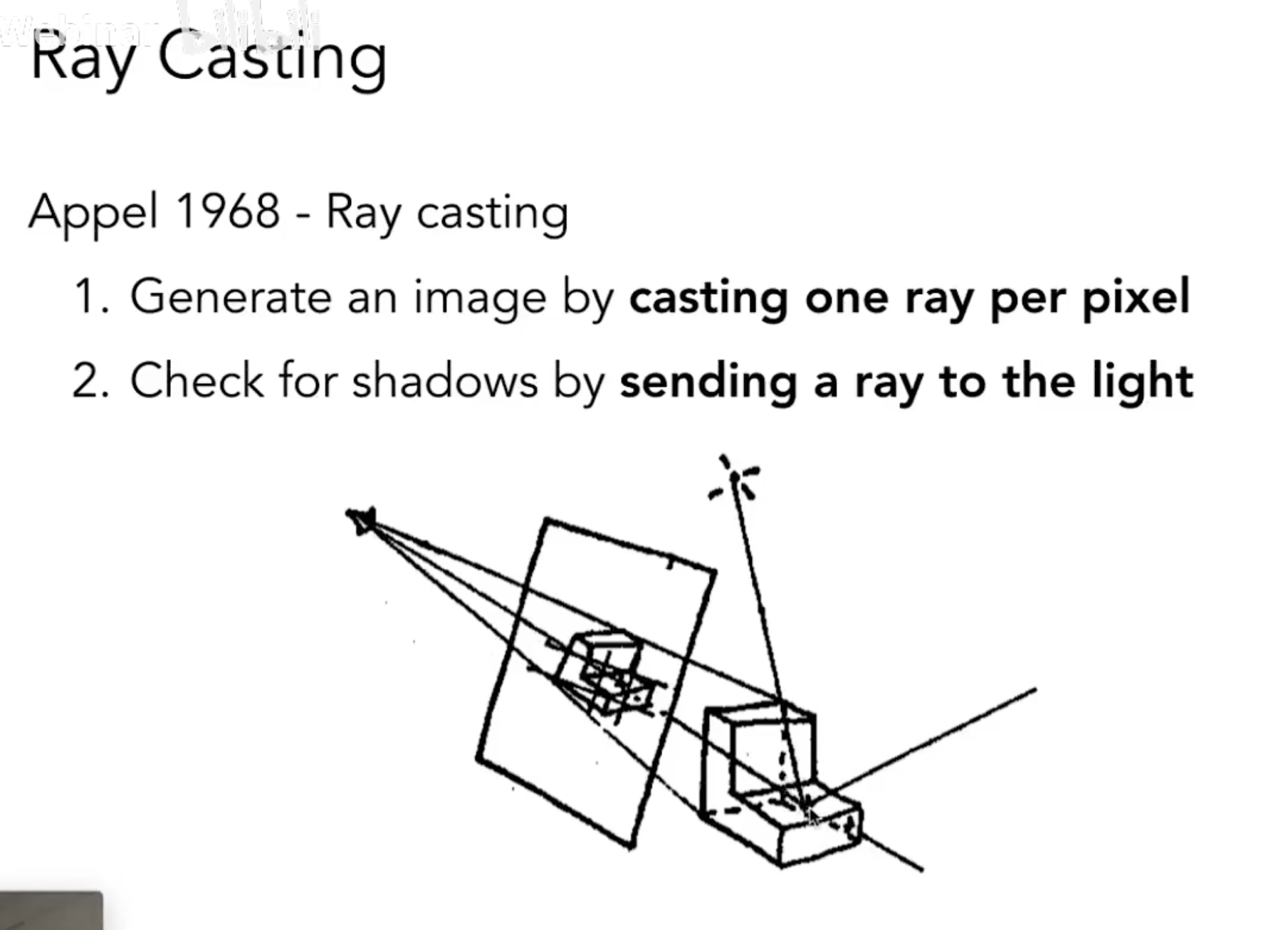
Ray Casting 光线投射
1.Generate an image by casting one ray per pixel通过每像素投射一条光线来生成图像
2.Check for shadows by sending aray to the light通过向灯光发送光线来检查阴影
在光线投射中,记录每一根光线碰到的第一个物体closest scene,那么就完美的解决了深度测试的问题,不需要再考虑深度测试。
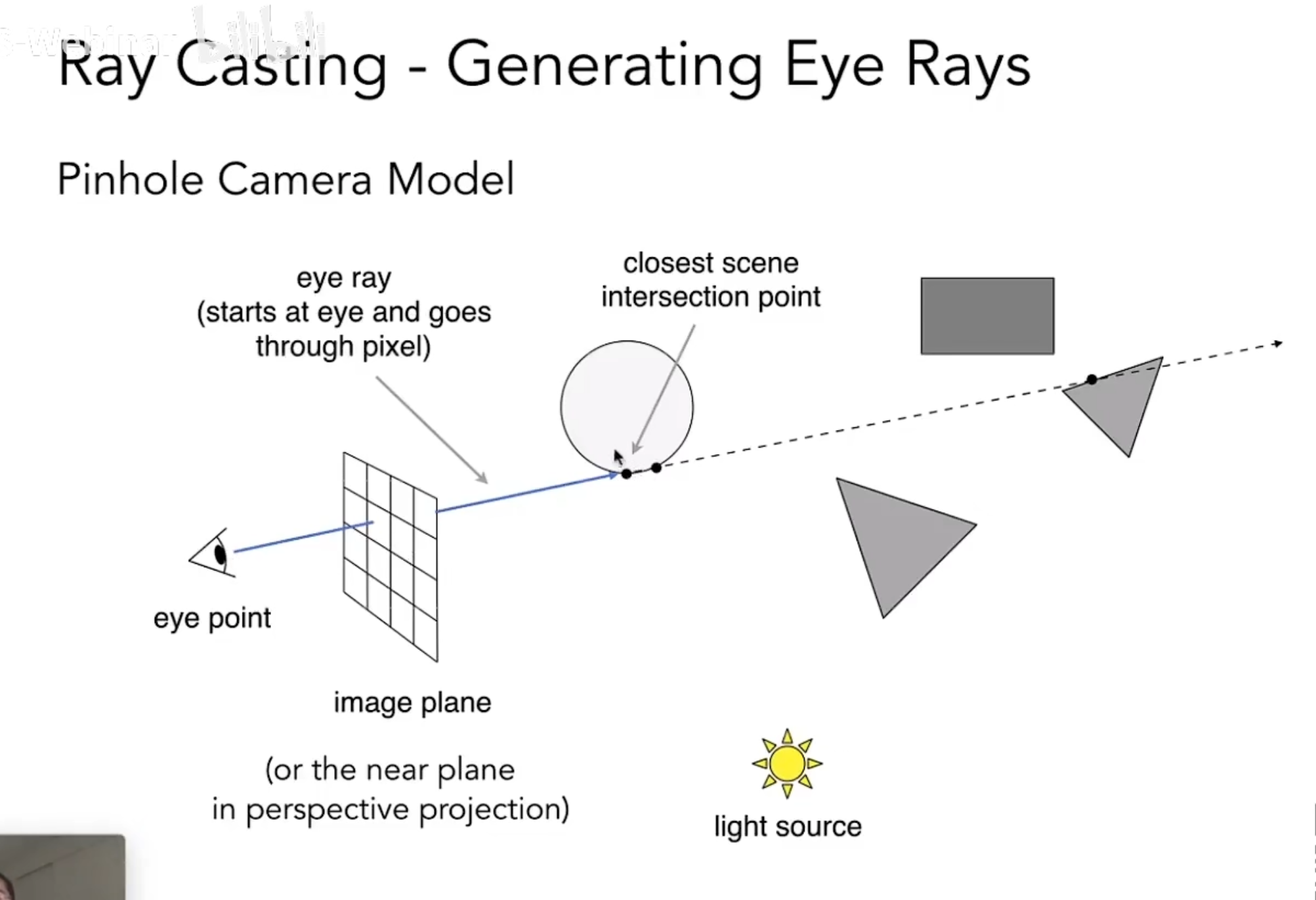
找到一个交点之后,我们考虑这个点会不会被照亮,然后从这个点连一条线到光源,如果路径上没有阻挡,那么就可以说明这点被光照亮了,再利用法线进行着色Shading
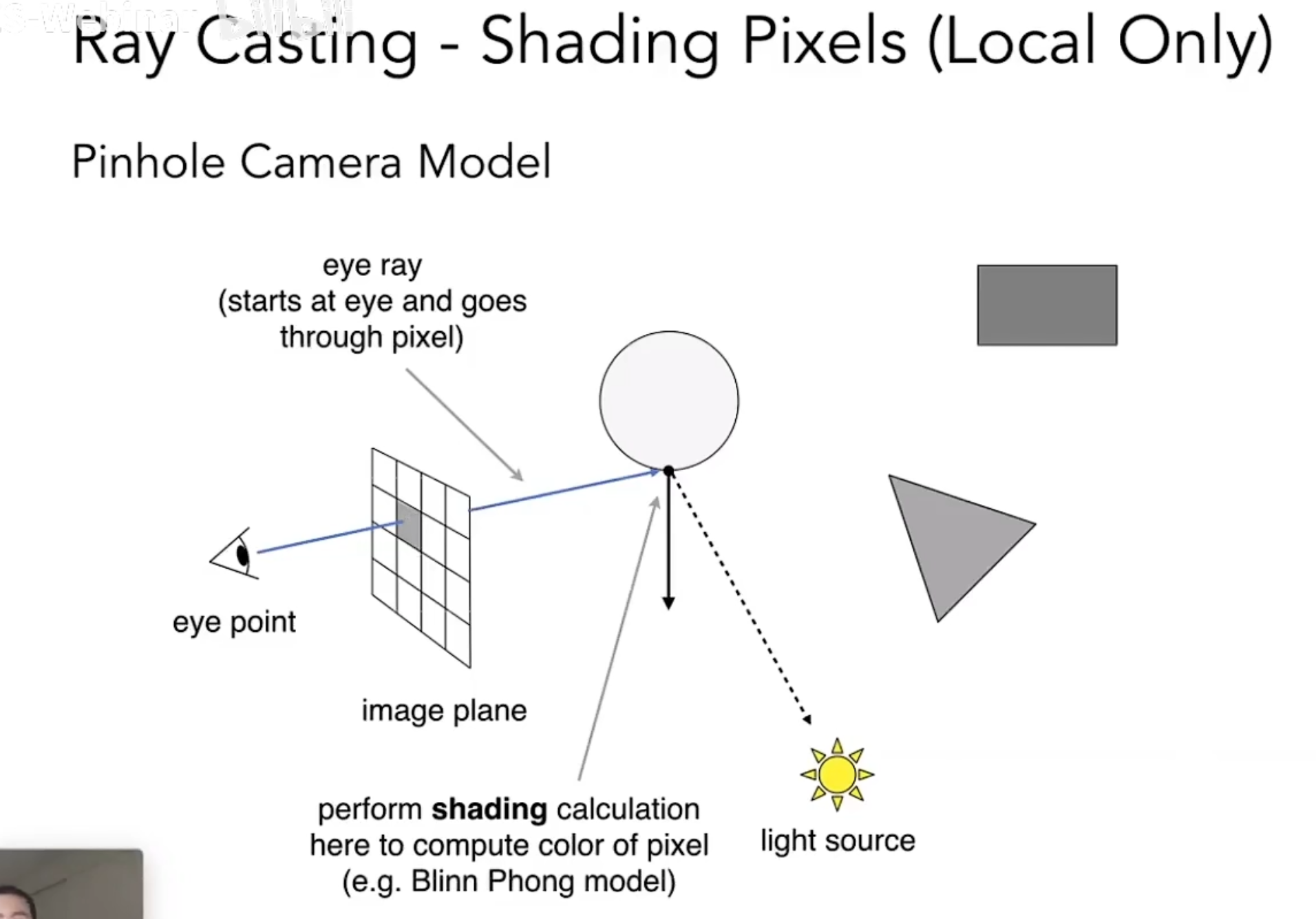
这种方法光线还是只反射了一次。
Recursive(Whitted-Style) Ray Tracing
在光线投射的基础上,我们把从像素出发的点在碰到物体之后进行反射和折射。
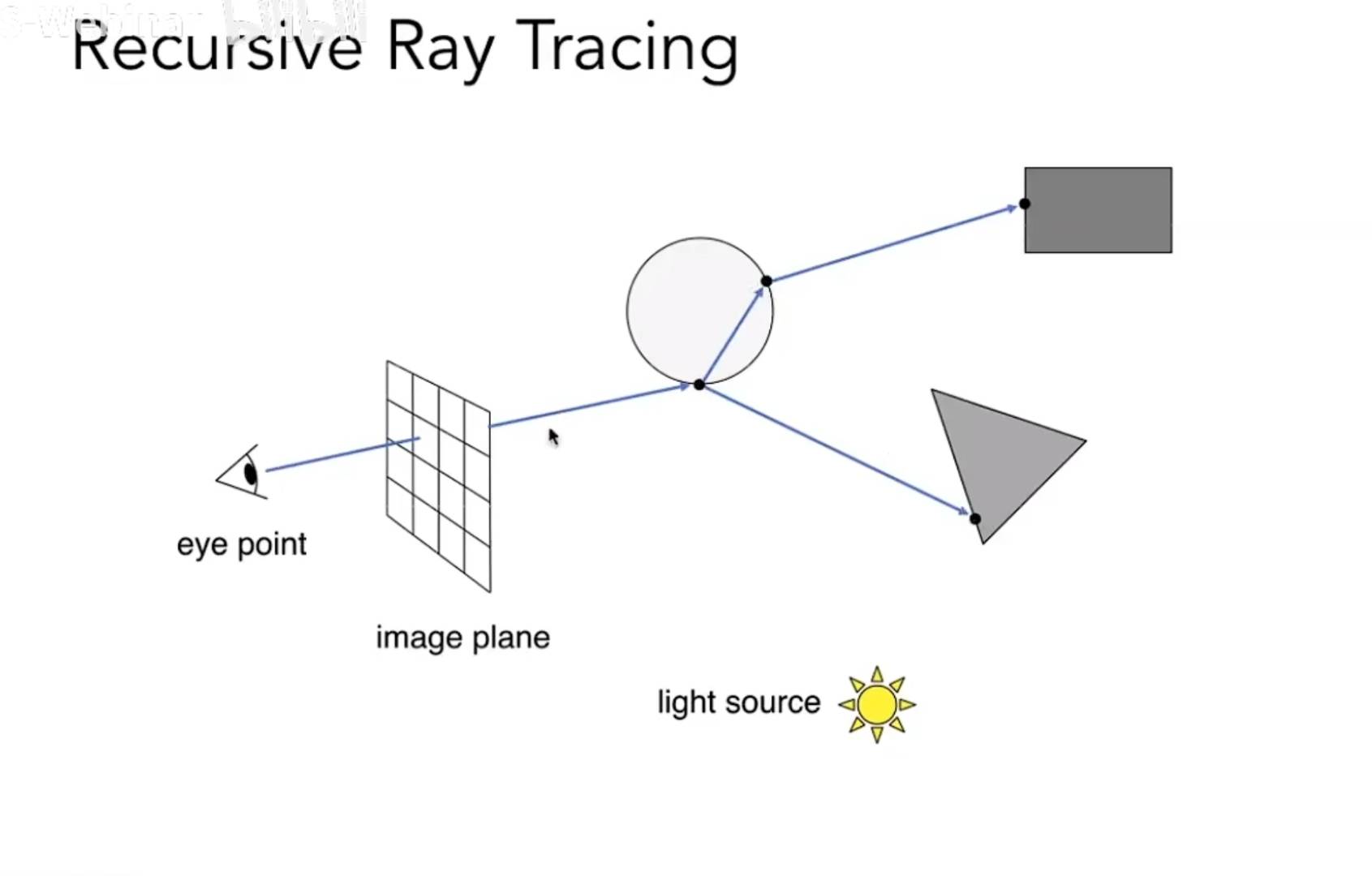
最后的着色则由各个点的着色的加权叠加组成,每一个点都需要计算它的shadow ray
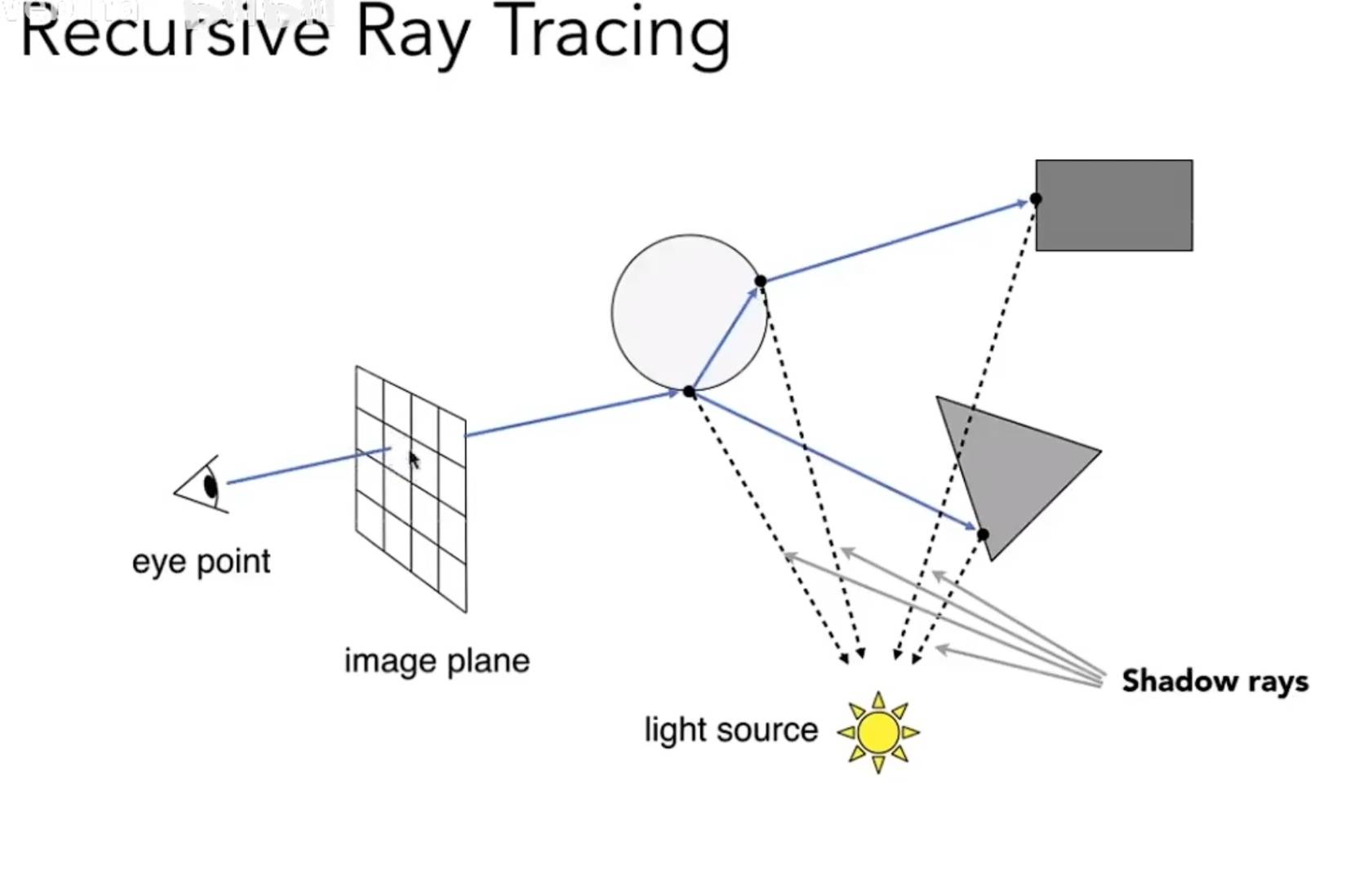
问题一:Ray-Surface Intersection(交点)
Ray is defined by its origin and a directino vector
光线定义为一个起点和一个方向向量
光线的方程:
\[Ray: r(t)=o+td,0<t< \infty \]
与最简单的图形球的交:
球:
\[p:(p-c)^2-R^2=0 \]
若相交,那么交点会满足两个方程,我们把光线的方程带入球的方程:
\[(o+td-c)^2-R^2=0 \]
然后解时间t,需要满足:
1.t是正的
2.t不是虚数
3.t得是最小的
与隐式表面的交:
隐式表面就是L:\(p:f(p)\)表示的一个方程
带入得到:
\[f(o+td)=0 \]
同样的需要满足,t是正的,t不是虚数
目前的求根的方法已经很发达了,所以求根不是问题
怎么计算交点?
Simple idea:jusr intersect ray with each triangle
直接计算每一个三角形与光线是否相交。(很慢,但有效)
把问题分解为两个小的问题:
1.光线经不经过三角形所在平面
2.光线与平面的交点在不在三角形内
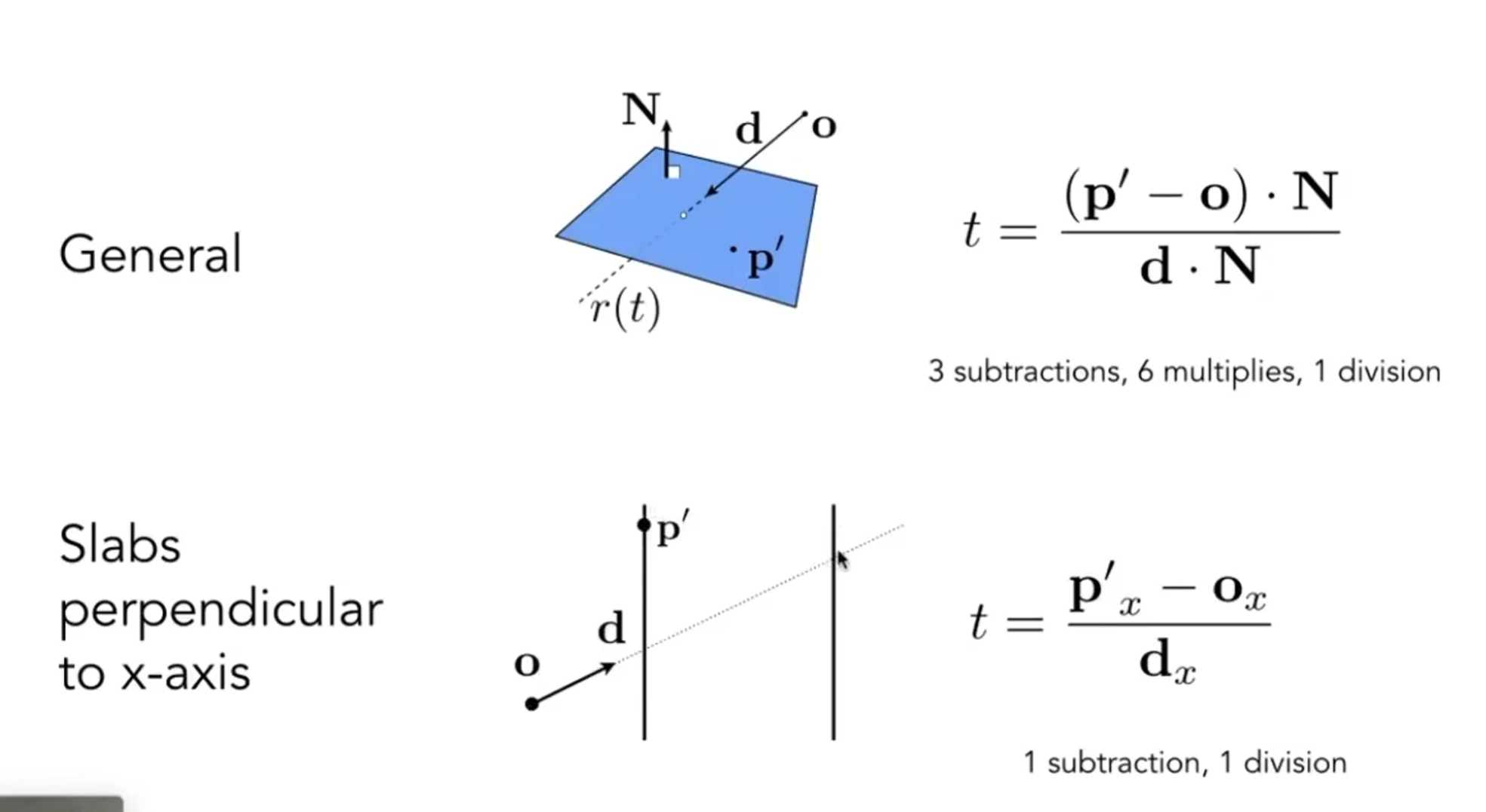
三角形所在平面
点法式
平面方程为
\[(P-P’)\cdot N=0 \]
求交点
简单的方法
\[(o+td-P’)\cdot N=0 \]
\[t=\frac{(P’ -o)\cdot N}{d\cdot N} \]
Check:$0<t<\infty $
交点是不是在三角形内
交点与顶点构成的向量与边的向量进行叉乘
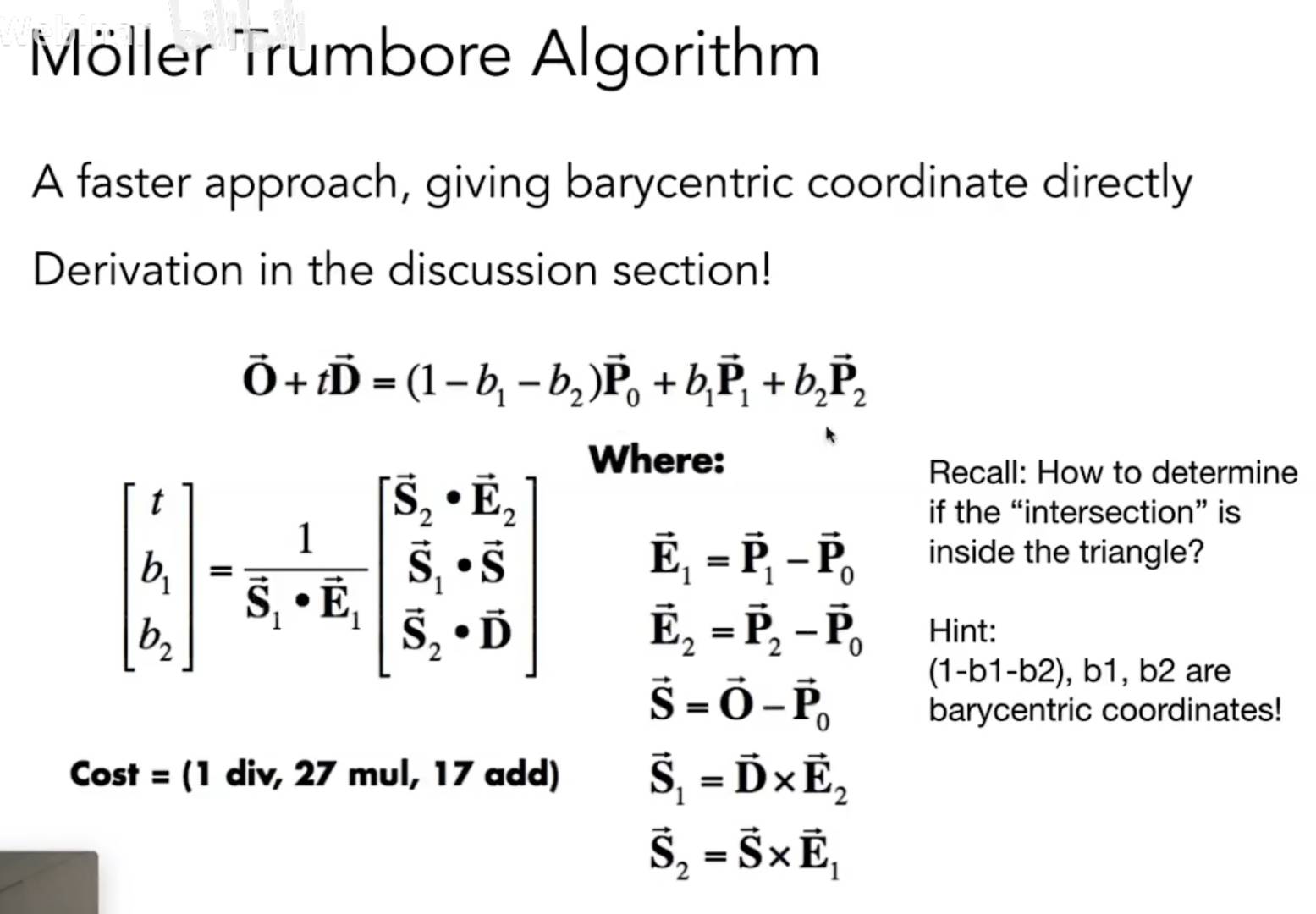
快速的方法
一步到位 Moller Trumbore Algorithm
其中\(\vec O+t\vec D\)就是光线的位置,如果在三角形内,那么一定可以用三角形的重心公式写出来,又这是三维向量,那么就是三个未知数,三个方程,可以直接解线性方程组,就能判断是否相交。甚至可以直接计算行列式来进行在否的判断,而不需要计算点的具体位置。用到克莱默法则
问题二:加速求交(从三角形数量上)
Bounding Volumes 包围盒
1.Object is fully contained in the volume.
2.If it doesn’t hit the volume, it doesn’t hit the object.
3.So test BVol first, then test object if it hits.
如果碰不到包围盒,那么肯定碰不到物体,所以首先测试包围盒,如果能碰到包围盒,再测试物体本身。
Axis-Aligned Bounding Box,使用三个对面来唯一确定一个长方体,使用AABB来当作包围盒,与光线进行求交。在二维时候,对于两个对面,我们可以计算出光线进入面和出面的时间(可能为负数),把光线和经过的两个线段求交集,得到的就是光线进入和出去光线的路径。
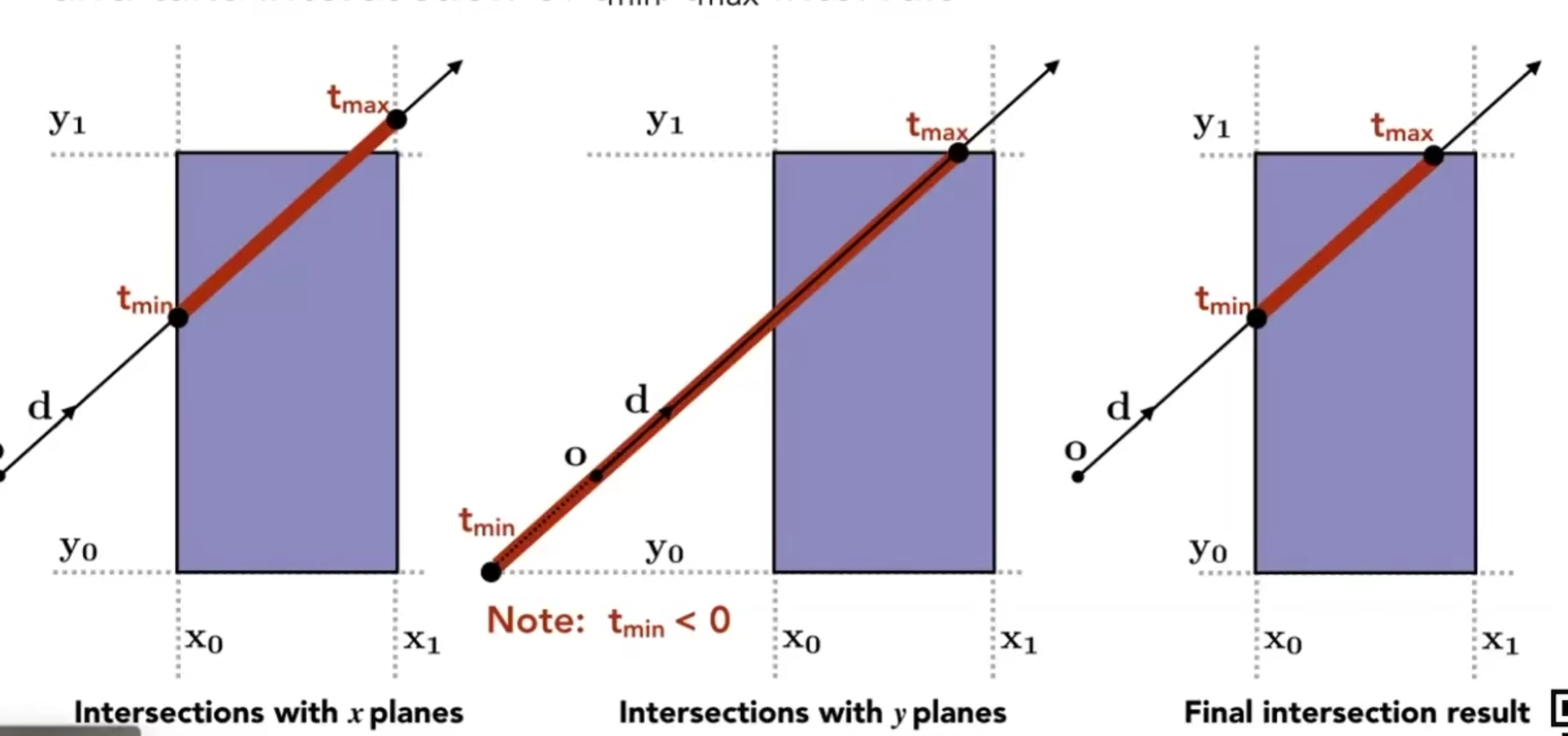
拓展到三维:只有当光线进入了所有的三个对面后,再出某一个对面。也就是光线进入三个对面的时间都小于离开任意一个对面的时间。也就是最大的进入时间小于最小的离开时间时,说明光线进入了AABB。

得到光线与AABB有交点:

为什么使用AABB?计算简单
Preprocess - Build Acceleration Grid
通过画小网格,来细分包围盒。找出可能有物体(边缘)的格子,然后进行光线追踪。
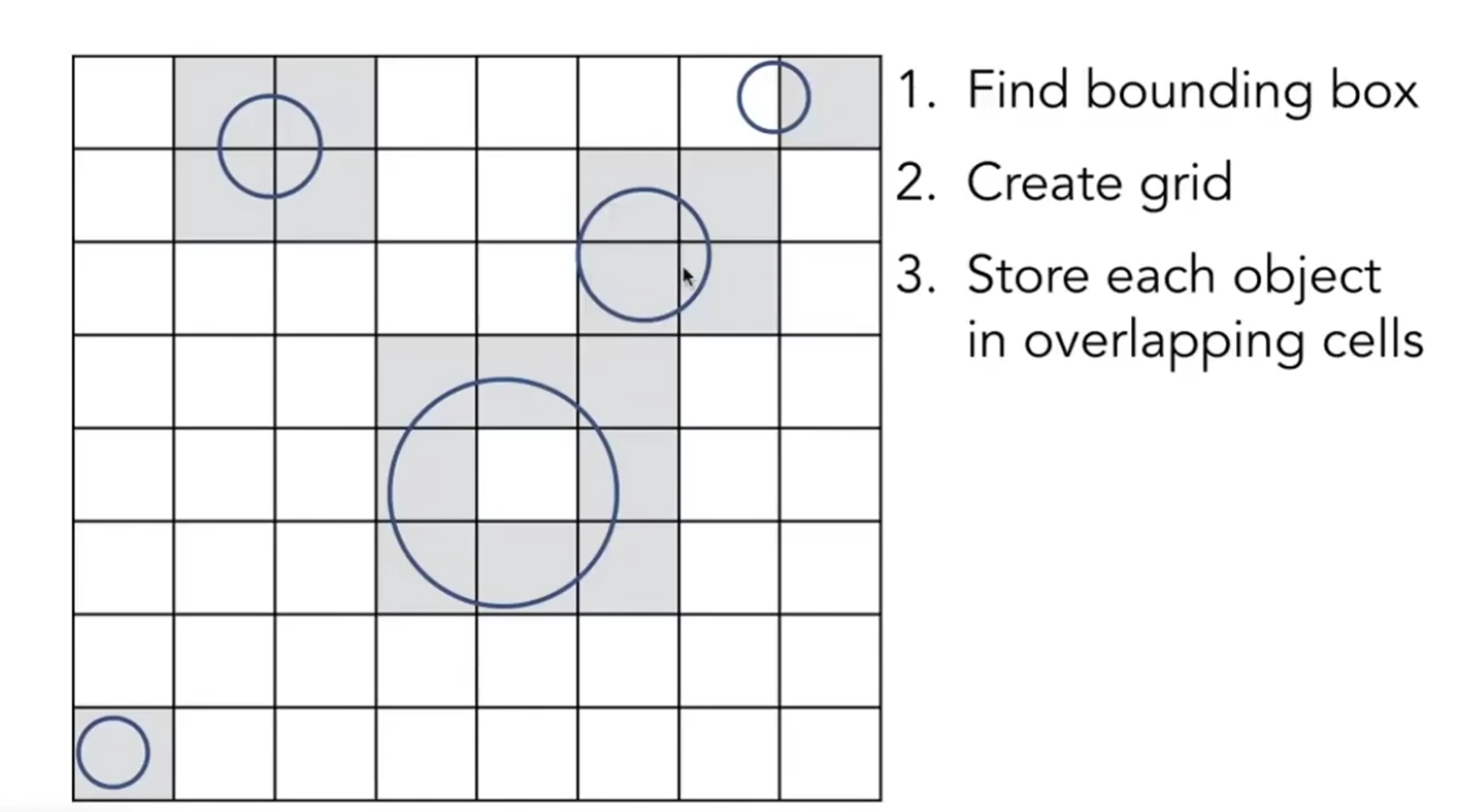
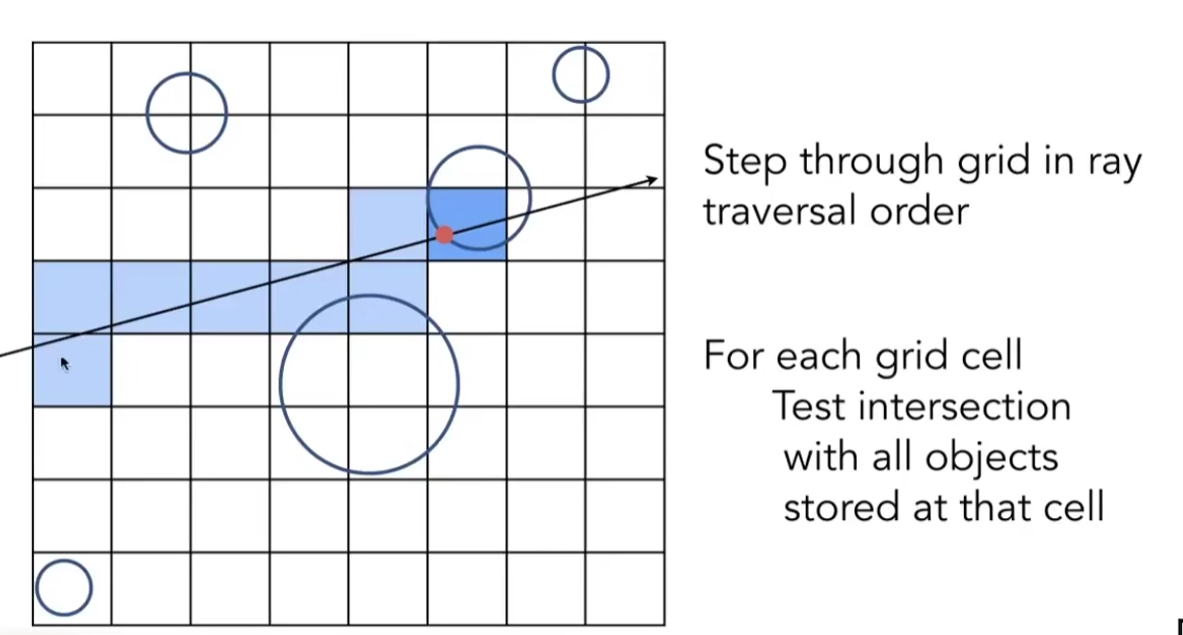
那么对于划分格子也相当有技术,太稀疏和太密集都不太好,一般使用物体的数量乘以27(虽然没什么意义hh)
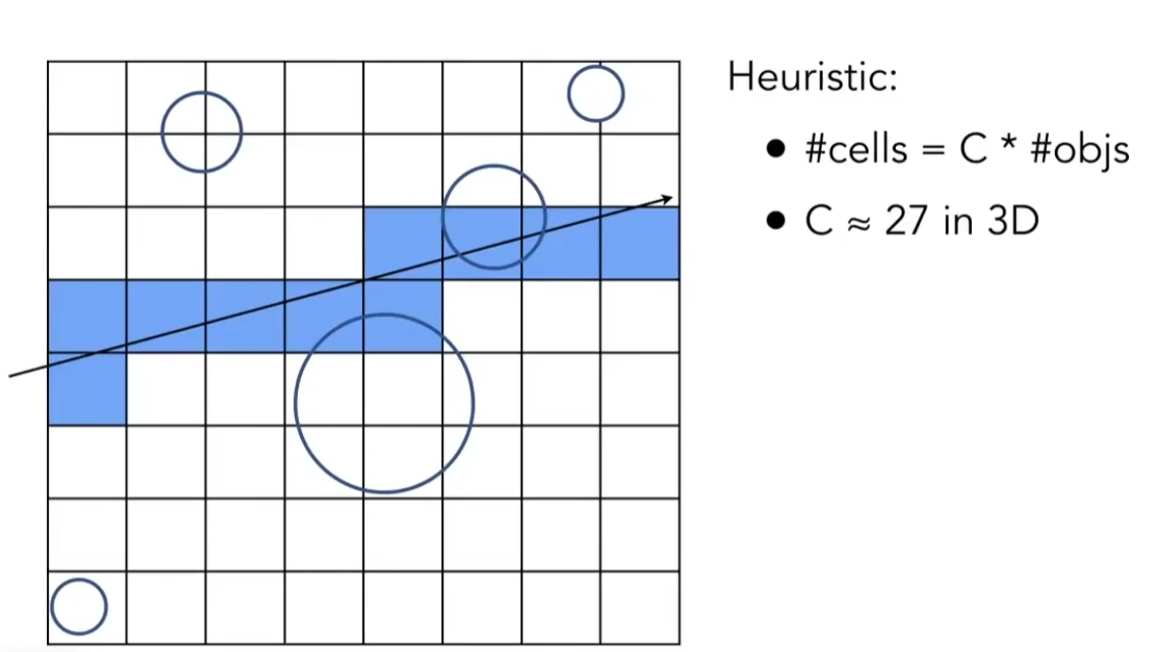
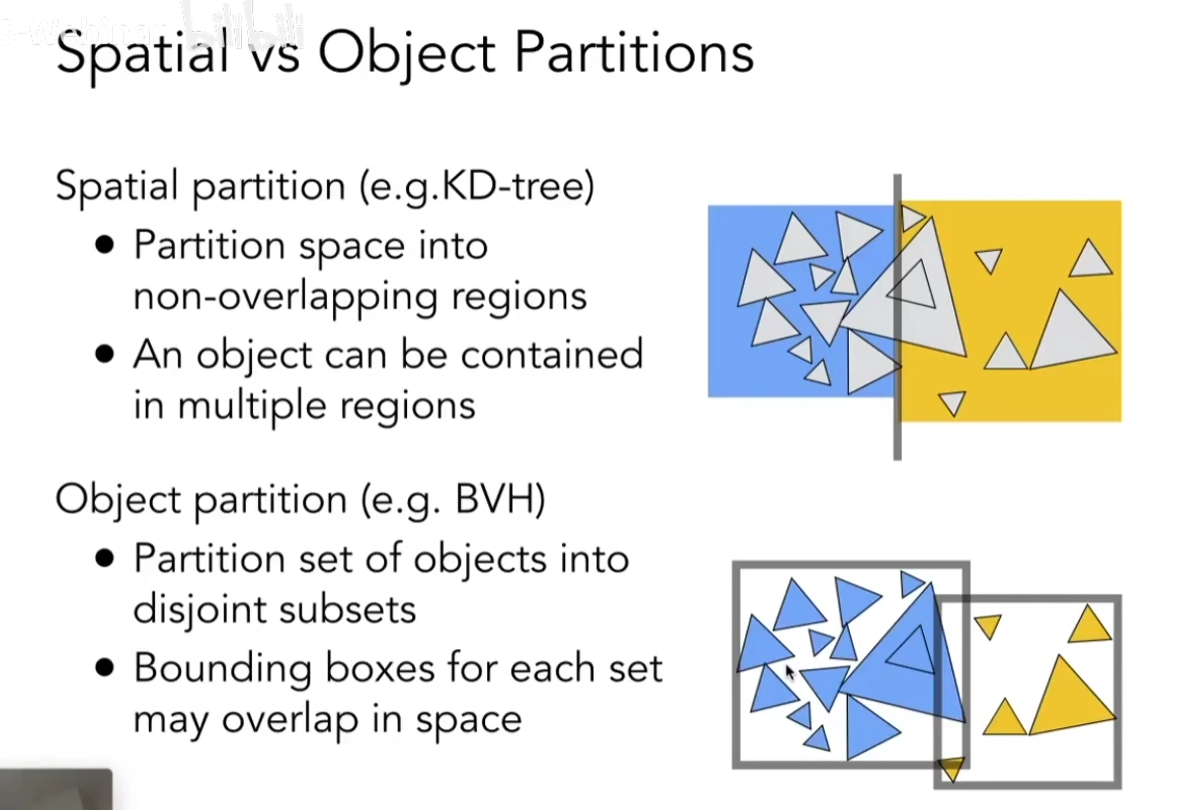
Spatial Partitions
空间划分,因为空旷的地方出现一个小的物体,会导致网格划分非常的低效。使用空间划分来解决这个问题。
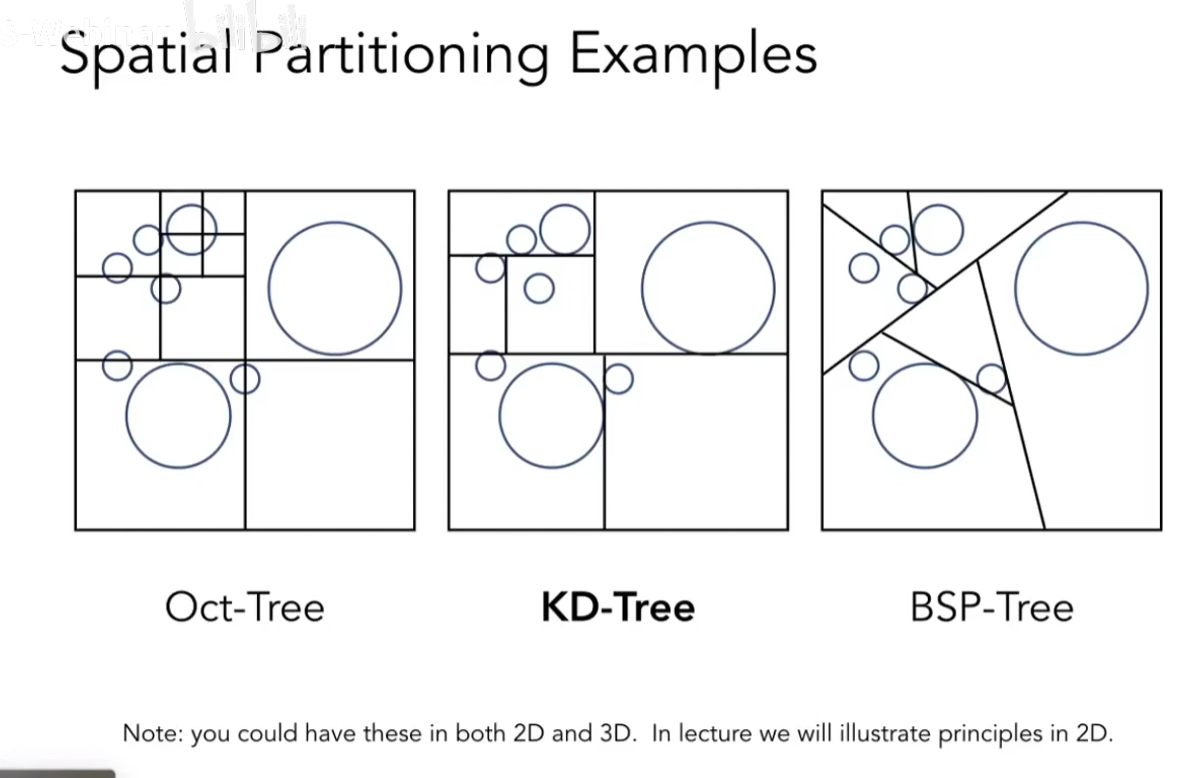
第一个是八叉树,进行细分,并且给一个停止细分的规则,比如格子中的物体数量小于某个数。但是八叉树的性质不好,因为细分度和维度呈几何次数上升。2 4 8
第二个是每一次只在格子里沿着某一个轴,进行划分,但是保证划分是交替出现,x\y\z。这么进行不会导致非常高的复杂度,而且保存了二叉树的原理。
第三个是BSP树,不满足AABB
我们主要学习KD-Tree
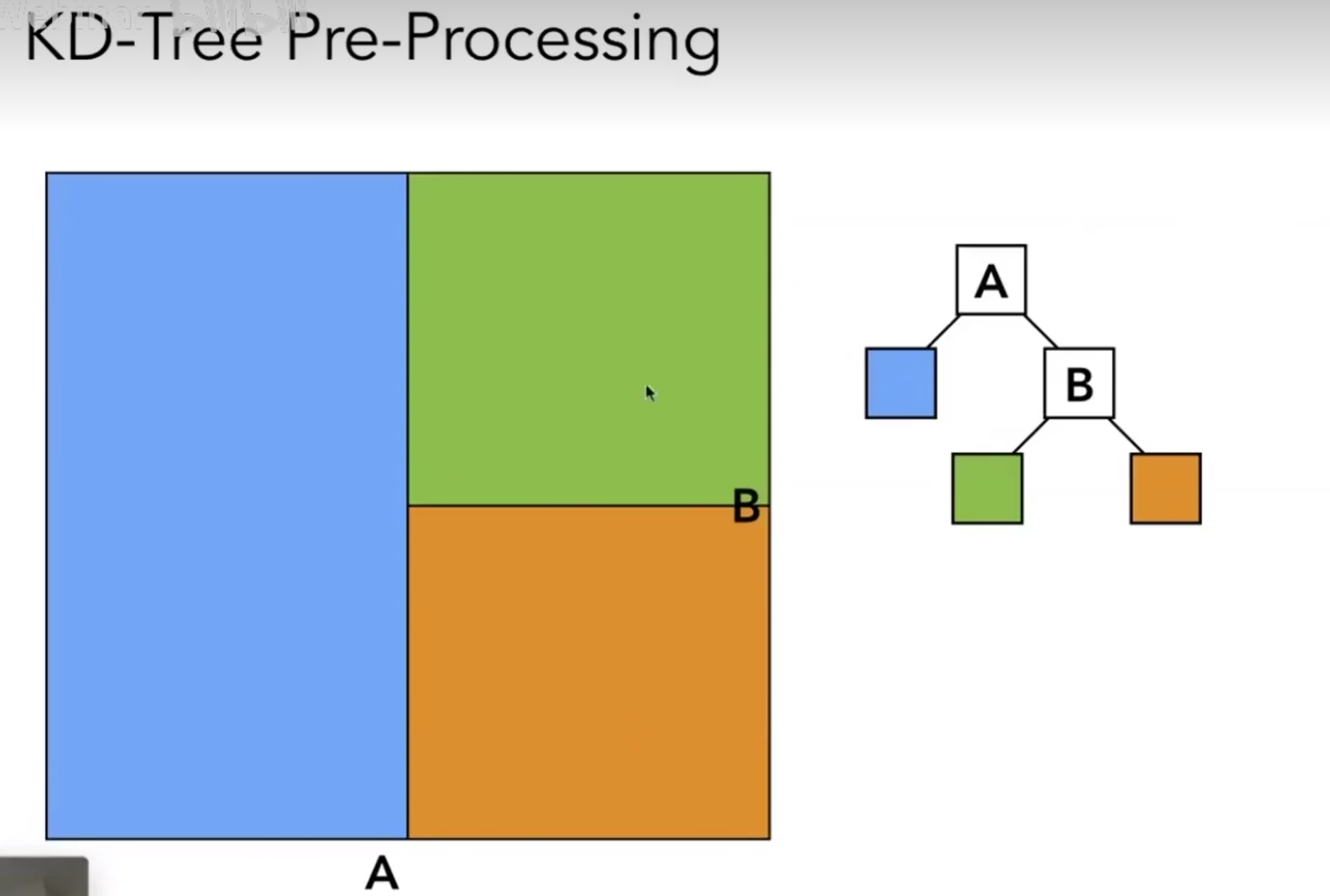
进行空间划分,但是对于左边的蓝也需要进行相同弄的操作。会形成一棵二叉树。实际的数据只存储在叶子节点上。进行计算时,首先对最大的包围盒进行计算:
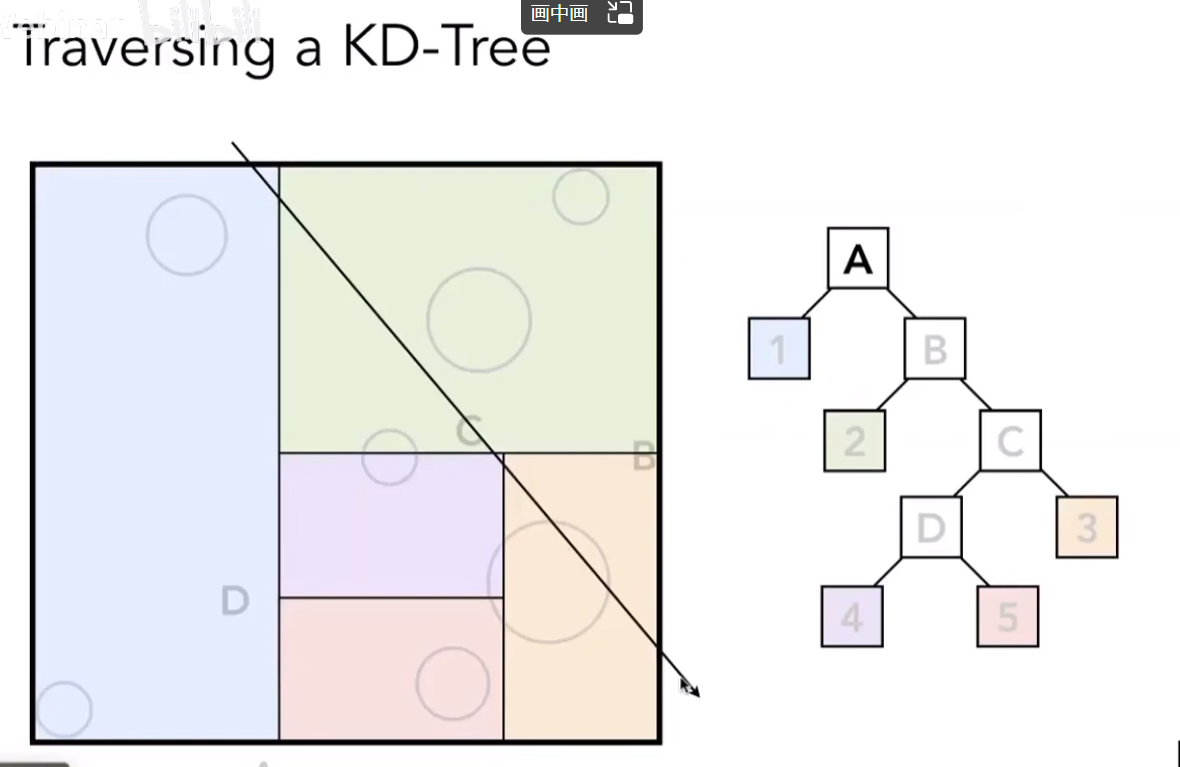
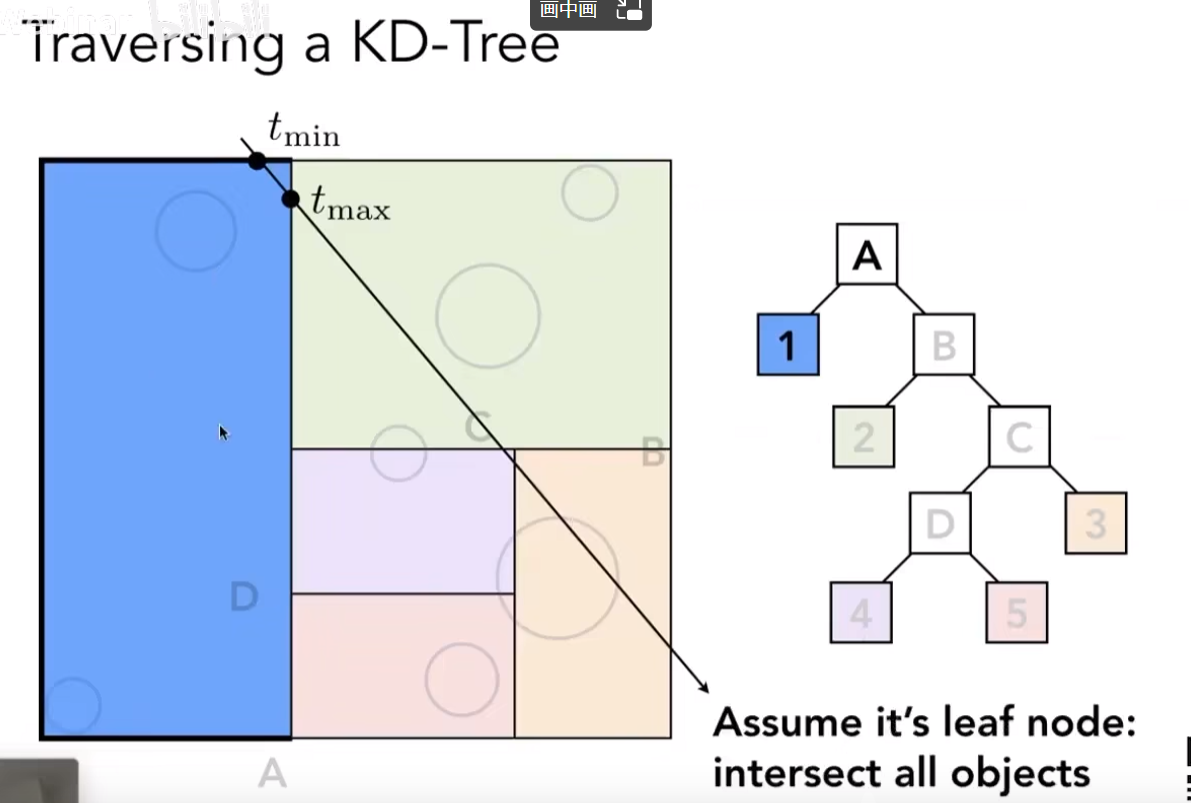
发现光线和左边的叶子节点有交点,那么开始计算光线和左边包围盒中的物体进行求交。
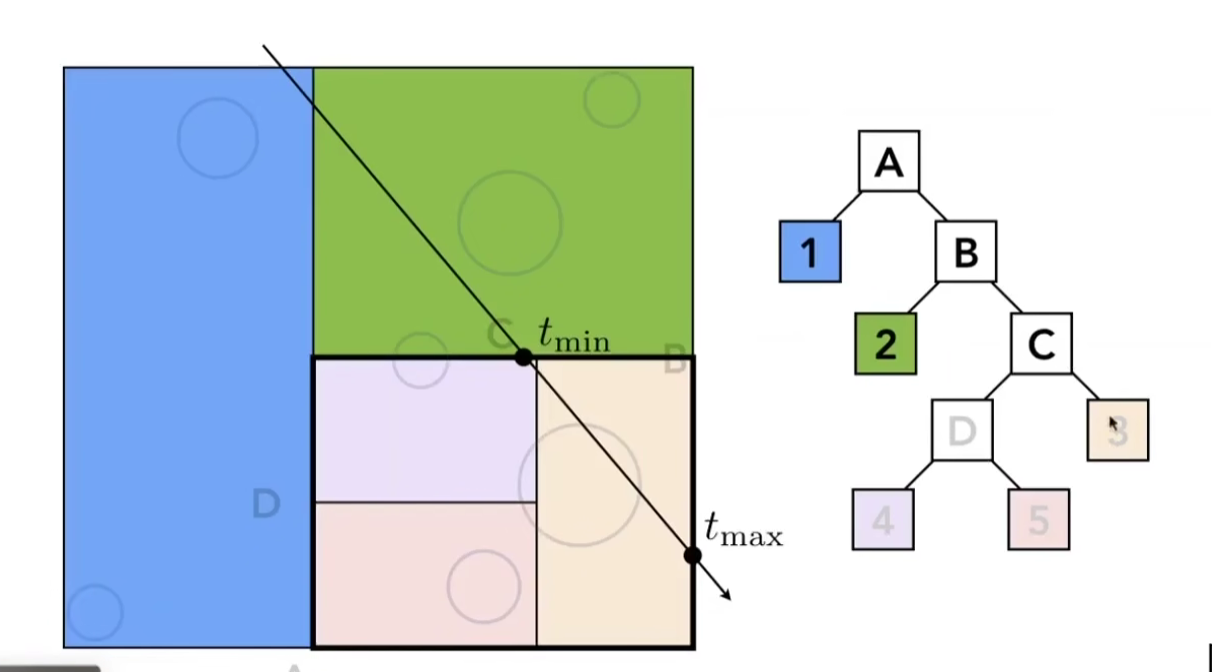
然后继续搜索。计算所有和光线相交的叶子节点。
问题出现了,两个包围盒会同时包括一个物体,那么会产生极大的消耗。使用BVH(Bounding Volume Hierarchy)来解决这个问题。在KD的基础上,进行优化不再划分空间,而是对物体进行划分:把物体分为两堆,然后对物体堆进行包围盒的计算。
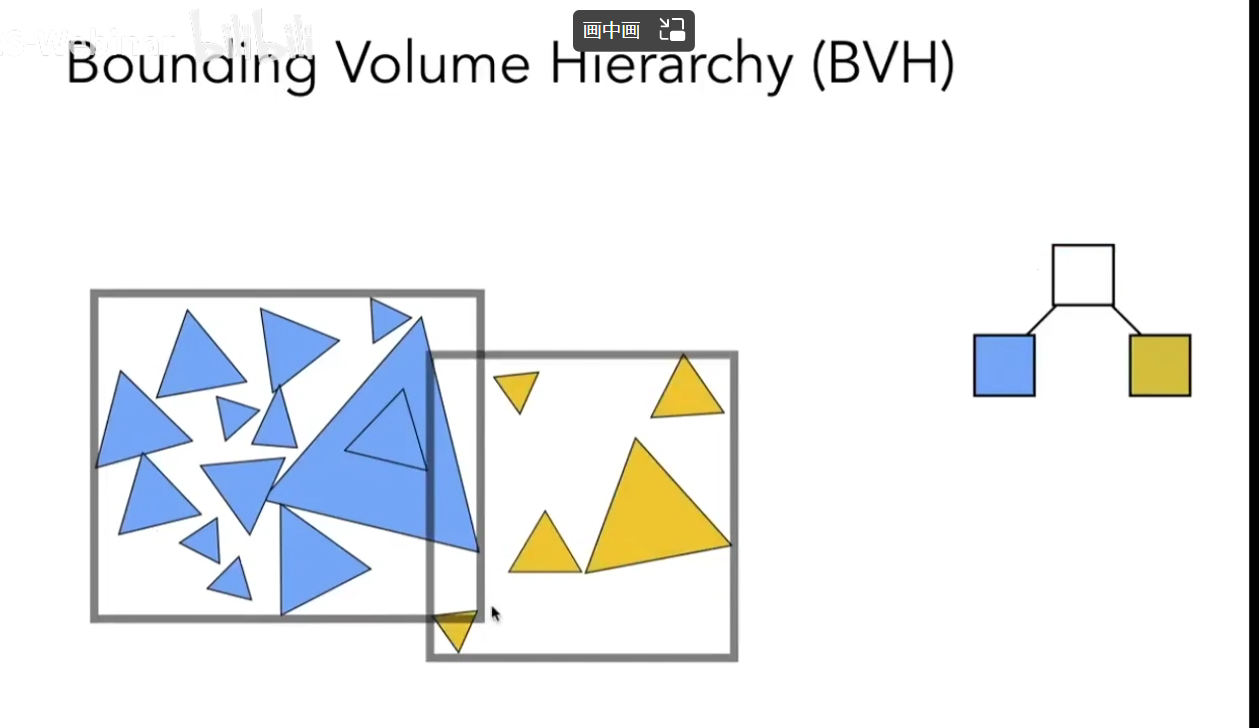
但是BVH划分的包围盒存在相交,这也是另一个问题,但是比KD-Tree得到的划分更加的好。BVH的怎么划分就成了重要的问题。
BVH的划分:
把三角形进行排序,然后取中间的三角形进行划分,可以使得这个树更加的平衡,也就意味着树的深度可以达到最小。算法:
给一列n个的数,你要找第i大的数,你可以在o(k)进行处理(快速选择算法)。BVH的递归算法:(伪代码)
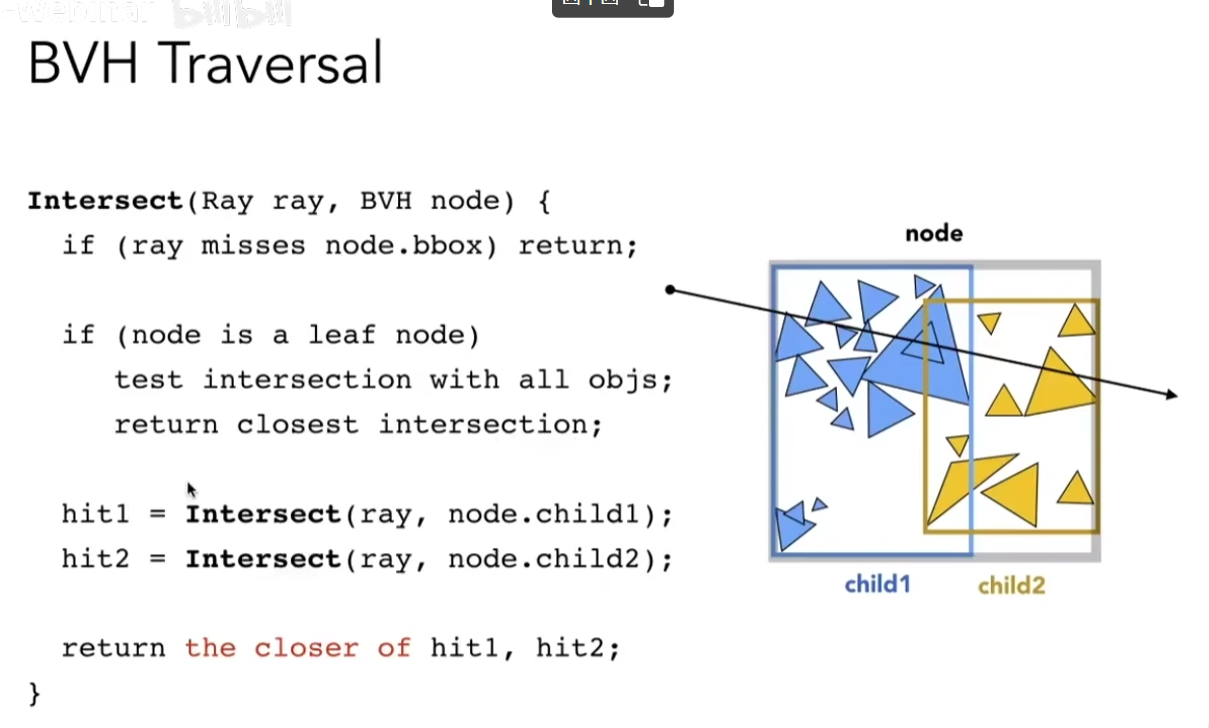
KD-Tree与BVH