第二课——线段树
上一节课讲了树状数组,也介绍了树状数组的优点与不足,这里简单回顾一下。
**优点:**树状数组的代码非常简短,易于实现,被刘老师亲切的称为IO选手的"HelloWorld!",就是因为代码短。
**缺点:**树状数组的缺点也非常的明显,只能处理单点修改区间查询或者区间修改单点查询的问题(以较高的效率)。而区间修改区间查询的问题没有办法很优雅的解决,于是引出了线段树。
线段树
先来看一个问题:
7-1 张煊的金箍棒(2)
张煊的金箍棒升级了!
升级后的金箍棒是由几根相同长度的金属棒连接而成(最开始都是铜棒,从1到N编号);
张煊作为金箍棒的主人,可以对金箍棒施以任意的变换,每次变换操作就是将一段连续的金属棒(从X到Y编号)改为铜棒,银棒或金棒。
金箍棒的总价值计算为N个金属棒的价值总和。其中,每个铜棒价值为1;每个银棒价值为2;每个金棒价值为3。
现在,张煊想知道多次执行操作后的金箍棒总价值。
输入格式:
输入的第一行是测试数据的组数(不超过10个)。
对于每组测试数据,第一行包含一个整数N(1 <= N <= 100000),表示金箍棒有N节金属组成,第二行包含一个整数Q(0 <= Q <= 100,000),表示执行变换的操作次数。
接下来的Q行,每行包含三个整数X,Y,Z(1 <= X <= Y <= N,1 <= Z <= 3),它定义了一个操作:将从X到Y编号的金属棒变换为金属种类Z,其中Z = 1代表铜棒,Z = 2代表银棒,Z = 3代表金棒。
输出格式:
对于每组测试数据,请输出一个数字,表示操作后金箍棒的总价值。
每组数据输出一行。
输入样例:
1 | |
输出样例:
1 | |
可以看到题目中非常明显的区间修改+区间查询的意图,这也是线段树的一道入门题目。接下来我来介绍这个神奇的数据结构。
构成
线段树由一个四倍原数组长的数组组成,对于数组中的元素也有着特殊的含义,但是比起树状数组来说要好理解多了。
首先我们不从数组层面来看这个数据结构,而是从一个二叉树,一棵完全二叉树。假设我们的原数组有8个数。那么线段数和原数组的关系就像这样:
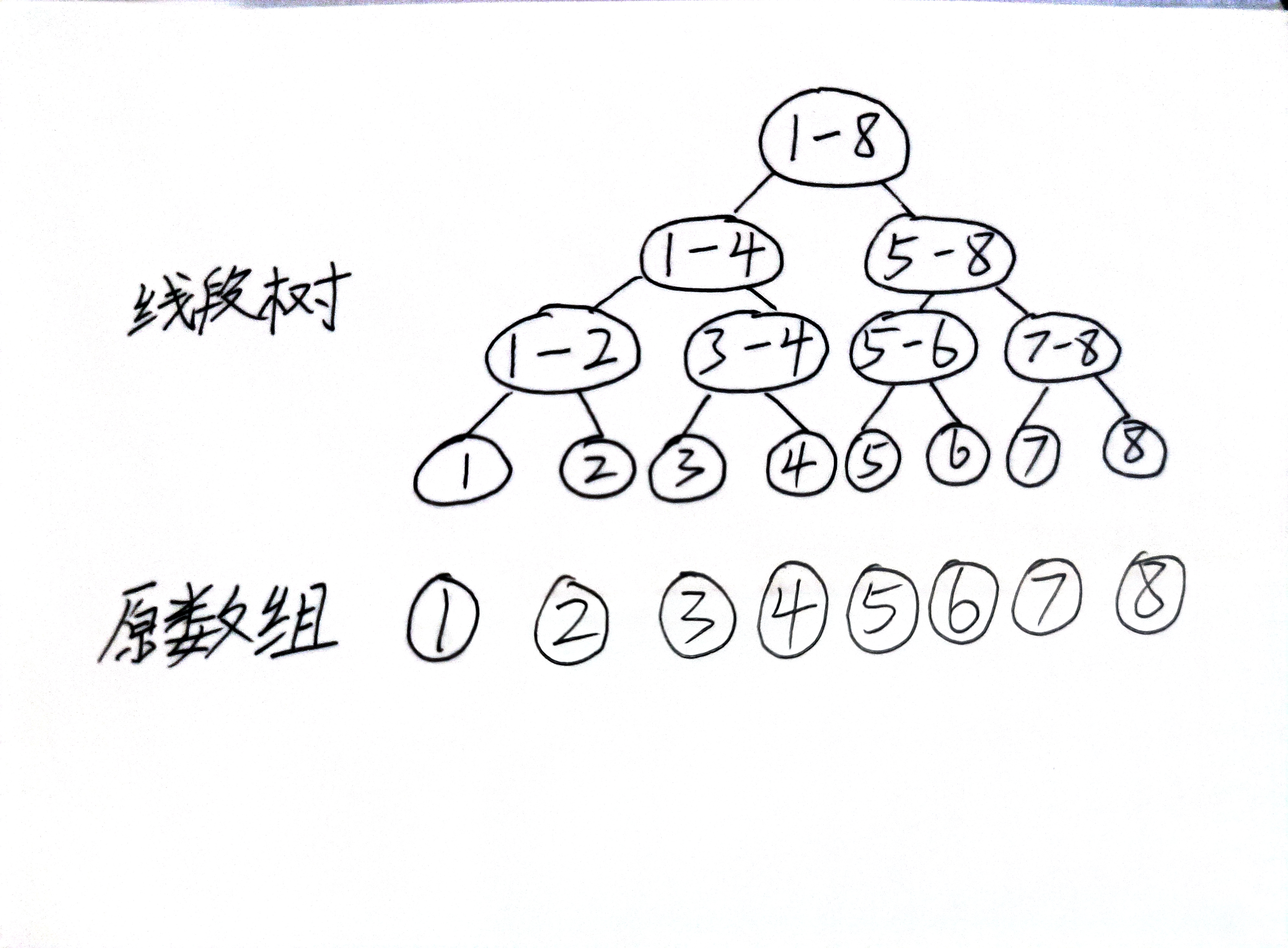
在线段树上的每一个节点表示对应区间的某个属性值,只要这个属性值满足区间的加法即可。
举个例子,这个属性值可以是区间和,可以是区间最值等等,这些具体的属性由题目来决定了,由于属性值的自由度极高,导致线段树在非常多的场合可以用于加速。
见过了线段树的二叉树形状,接下里给线段树一个数组的表示方式。这个也非常的简单:
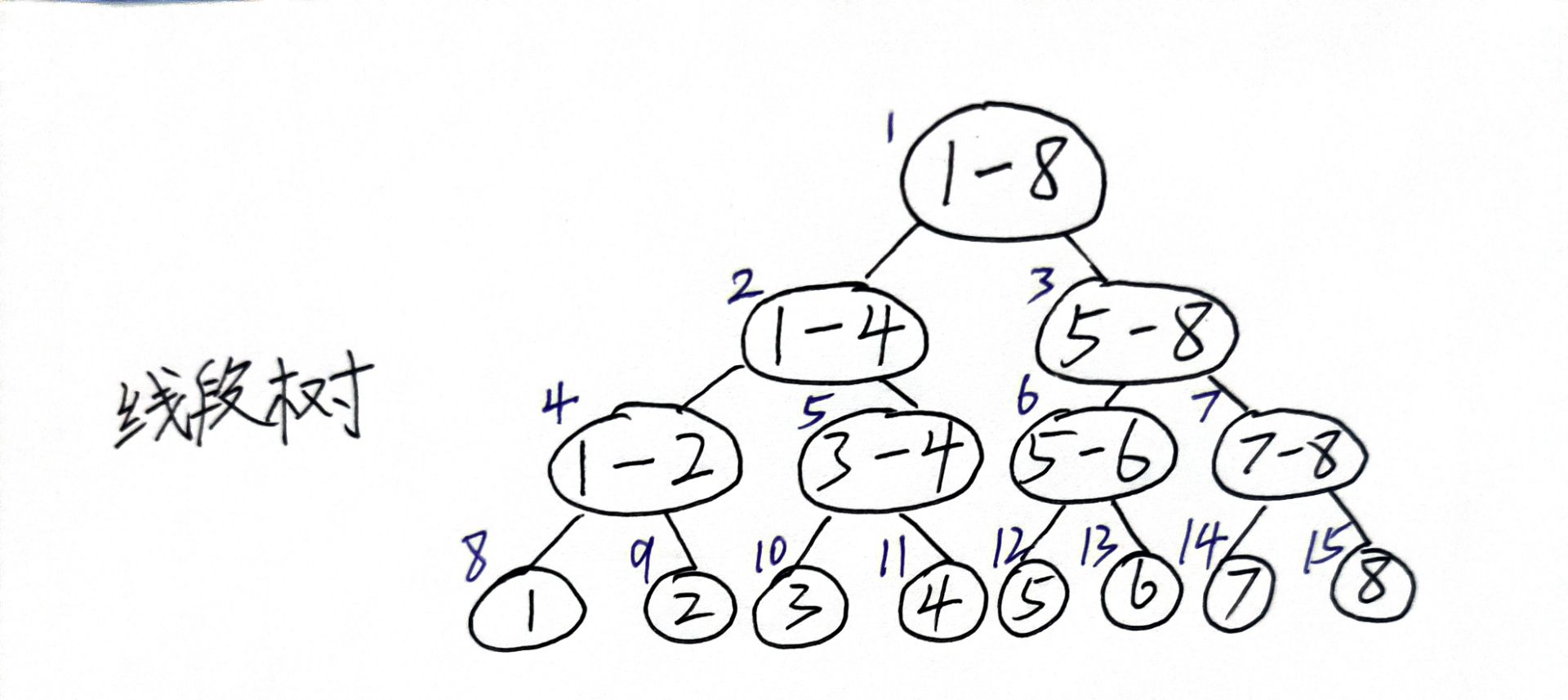
和《数据结构》中一致,从根节点开始为 1 ,宽度优先搜索的顺序升序标号。有了标号,我们就能用数组来存储这棵二叉树了。可是为什么我们需要四倍的原数组空间呢?
这里我们从长度为5的数组开始,来探讨一下这个问题。
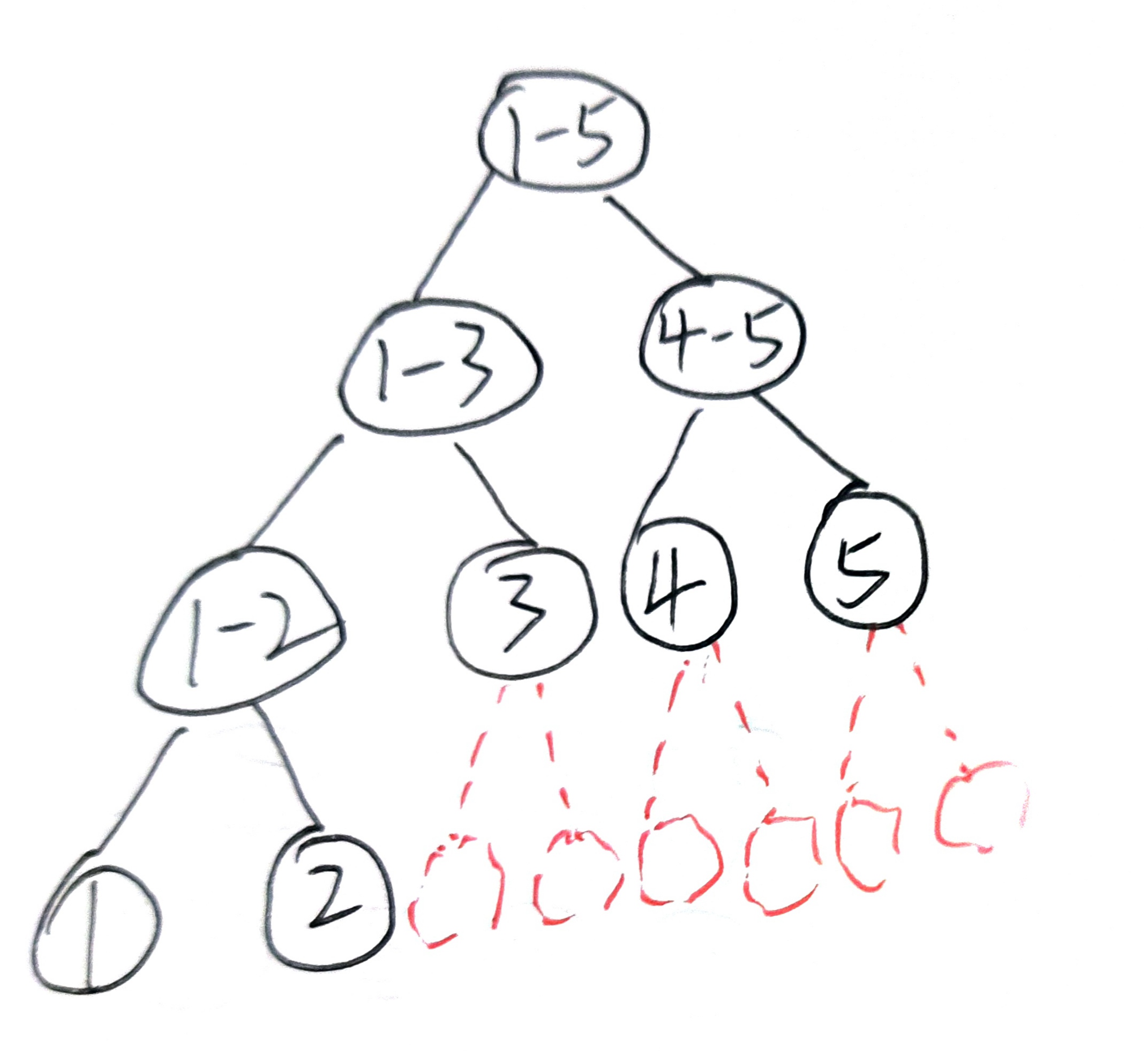
原数组长度为5,那么理论上黑色的节点已经够用了,但是我们使用的静态数组,一般会选择直接把完全二叉树所需的空间开出来,所以会用到最多四倍的空间。
左右子结点的访问
学过《数据结构》的读者可以跳过这块内容。
这部分比较简单,假设根的标志是1,那么左右子结点分别可以用以下两个函数访问:
1 | |
稍微解释一下访问右节点的操作,一个二进制数在左移动后最低位一定是0,那么这时候可以用1与该数位或,就能得到乘2加一的效果。
树的初始化
首先定义一下线段树的结构(代码层面)
1 | |
树的初始化是从原数组构造我们的线段树,以前面提到的题目为例子。节点的属性是区间和。
1 | |
可以发现线段树的构造是非常容易理解的。由于二分的存在它的复杂度也只是O(NlogN)。
单点修改
线段树的修改,相当于修改最下层的某个节点,它会影响到上层的非常多节点,依照树的初始化的想法,我们可以很容易的写出修改代码,这里不提供。
区间查询
首先有一个理论保障:线段树的每次查询不会超过O(logN)的复杂度。为什么呢?
- 任一连续区间至多由\(2log_2^N\)个子区间组成
-
- 原因:任一区间不在线段树同一层出现两个子区间,并且树高不超过\(logN\)
-
-
- 原因的原因:因为区间连续,所以如果在同一层出现了两个子区间,那么这两个子区间一定可以合成上一层的一个区间。
-
所以查询的复杂度有了保障。于是我们来讲查询的思路。
对于一个区间查询\([L,R]\),我们从根节点[0,4N]出发,进行二分查找,并把符合要求的区间上的节点都进行修改。Idea is pool show me the code!
1 | |
是不是超级简单?哈哈,刘老师说:“当年我们没有人教,没有题目刷的时候,学会了线段树就开始大杀四方,当时觉得是很稀奇的东西。你们今天倒好,随便就能学到如此有意思的算法。”
区间修改
这个就厉害了,不仅实现了区间修改,还引入了最高效的偷懒方式——lazy
思路是这样的:我们修改一个区间的时候,如果要把值给到每个受影响的节点,会非常的麻烦,并且涉及到多次修改时,程序的复杂度会较高。但是仔细想想,我们线段树上的节点不是能代表属性么,那是不是也可以记录修改的属性呢?于是lazy诞生了。
修改一个区间的时候,我们不修改对应的叶子节点,而是在最上层的区间节点上记录本次修改,并在查询的时候应用。
我们首先修改一下数据结构体:
1 | |
然后重写之前的各个方法:
1 | |
下面是应用lazy的函数的实现:
1 | |
到这里就讲完了,线段树我似乎没有进行多少理论的分析,大部分都是show you the code.但是线段树是一个抽象的,强大的优化工具,而不是一个算法。想要理解线段树,还需要自己去编码实现。这里提供完整的程序代码供你参考。
点击查看代码
1 | |
好好领悟线段树的节点属性吧。