计算机图形学笔记一——绘制直线的算法
绘制直线的算法
数值微分法
数值微分法(digital differential analyzer DDA)使用直线的增量方程来计算直线的下一个迭代点像素的方法。直线的微分方程:
$$
\frac{dy}{dx}=\frac{\Delta y}{\Delta x}=\frac{y_1-y_0}{x_1-x_0}=k
$$
得到迭代公式:
$$
x_{i+1}=x_i+\beta \Delta x
$$
$$
y_{i+1}=y_i +\beta \Delta y
$$
其中$\beta=\frac{1}{max(|\Delta x|,|\Delta y|)}$
也就是说,当斜率的绝对值大于1的时候,取y的步长为1,当斜率的绝对值小于1时,取x的步长为1。然后对非步长点进行近似,得到这样的代码
1 | |
再考虑斜率为0和斜率不存在的情况(垂直x轴和平行x轴),我们可以写出这样的代码,这便是DAA方法的实现。
DAA完整代码
1 | |
中点画线算法
不进行除法运算,减少计算量,使用一种近似的思想进行取样。下面两幅图中说明了这种算法的实施方法:
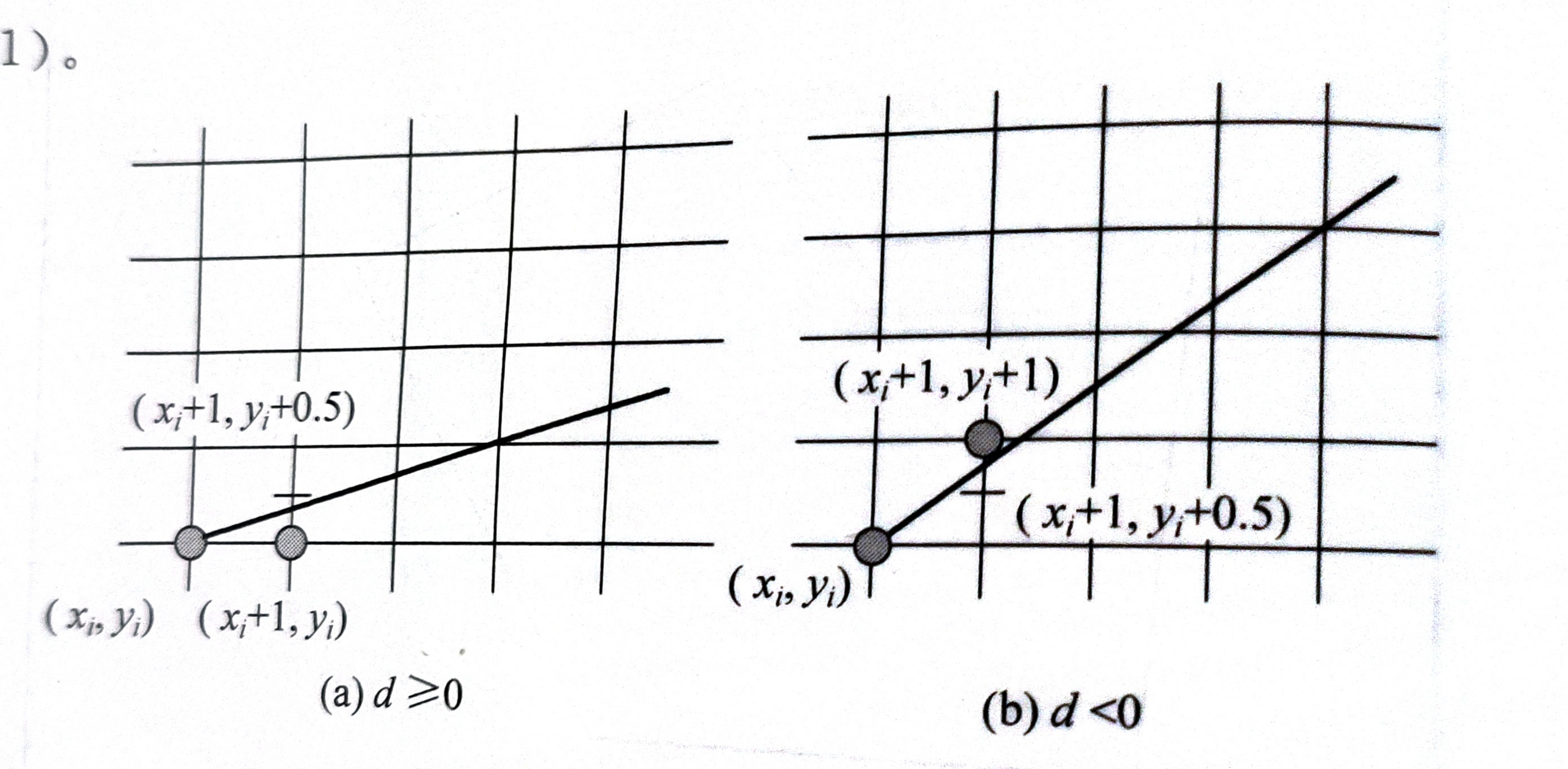
当曲线在一格的中间偏上时,使用上面的点作为采样点,当在中间偏下时,使用下面的一格。如此计算,便能绕靠斜率的除法运算。
实际实现方法:从左边的点开始,每次往右移动一格,计算这个点的中点处y与函数值的差,如果大于零,则y不变;反之y向上(下)移动一格。
那么有两个要求:
一、计算y移动的方向是上还是下
二、开始的点必须在左边
分析一下这个差值的计算:
$$
F(x,y)=ax+by+c=0
a=y_0-y_1
b=x_1-x_0
c=x_0y_1-x_1y_0
d=F(x_i+1,y_i+0.5)
$$
其中d也就是中点和直线的竖直距离,我们可以通过判断d的正负来进行采样。进一步分析
当d>=0时,下一个构造点为F$x_i+2,y_i$,那么
$$
d_1=a(x_i+1+1)+b(y_i+0.5)+c=d+a
$$
同理,当$d<0$时d$_1=F(x_i+2,y_i+1.5)$,即:
$d=a(x_i+2)+b(y_i+1.5)+c=d+a+b$
这样我们就得到了迭代方程,我们可以写出这样的代码:
1 | |
你可以在这里找到所有代码
TMP算法完整代码
1 | |
Bresenham画线算法
这是目前计算机图形学使用的最多的直线生成算法。在计算最佳逼近中使用的全部都是整数运算,可以大幅度的提升计算速度。
与TMP不同的一点就是,TMP是计算中点与直线上的点,而Bresenham是计算上下格子与直线竖直距离的差。也就是下面图像中的d2-d1
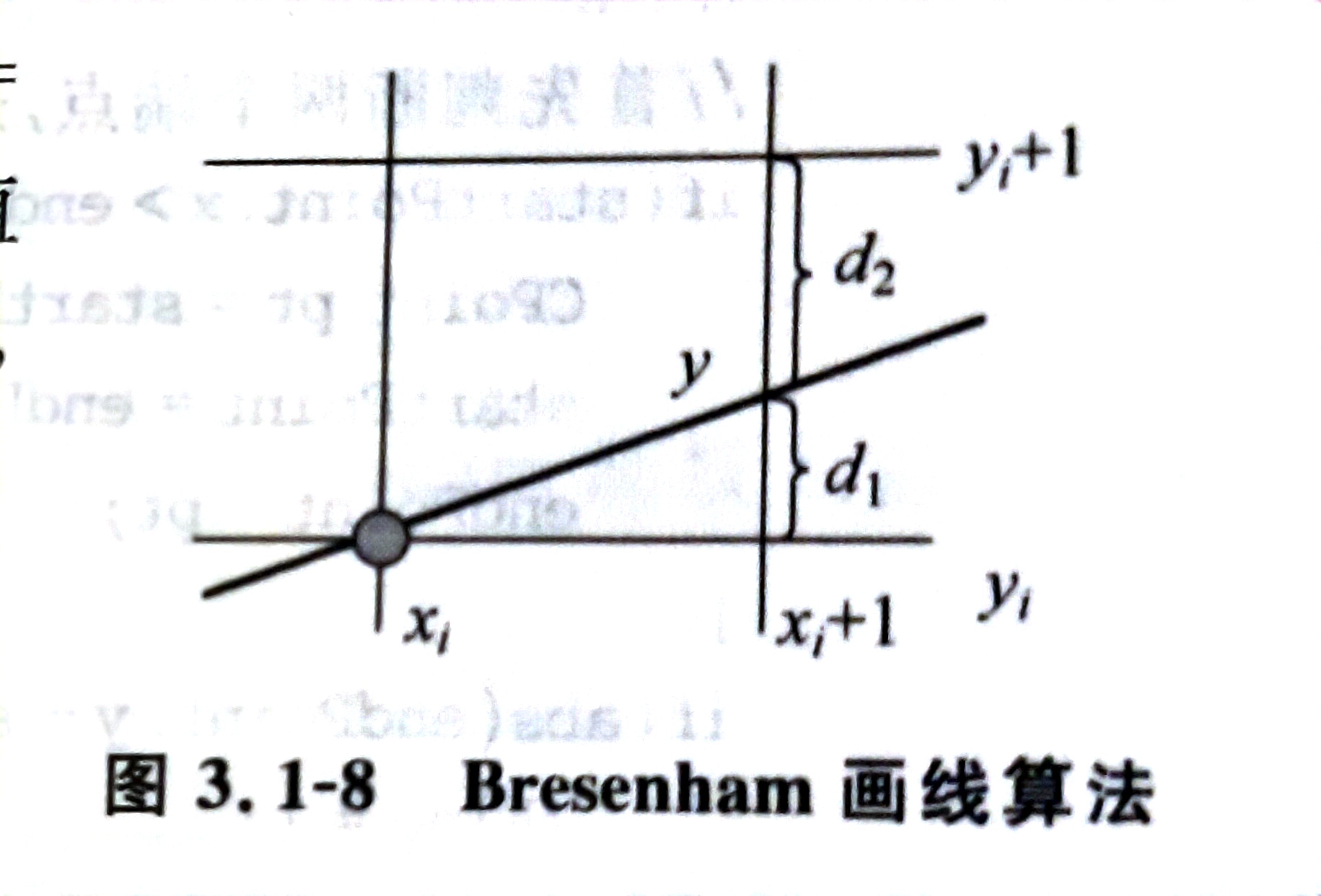
推导过程如下:
直线方程可以表示为(不管两种特殊情况)
$$
y=kx+b
k=\frac{y_1-y_0}{x_1-x_0}=\frac{dy}{dx},b=y_0-kx_0
$$
当 $ 0<k<1$时直线向正方向前进一个像素,对应的最佳逼近的 $x_{i+1}=x_i+1$, $y_{i+1}=y_i+1$or $y_i$
$$
y=k(x_i+1)+b
d_1=y-y_i
d_2=y_i+1-y
$$
令
$$
d_1-d_2=2y-2y_i-1=2(k(x_i+1)+b)-2y_i-1
$$
当 $d_1-d_2>0$时
$y_{i+1}=y_i+1$
当 $d_1-d_2<=0$时
$y_{i+1}=y_i$
魔法:当dx>0时,把 $d_10d_2$乘上$dx$,不影响整个式子的正负得到:
$$
p_i=dx(d_1-d_2)
$$
又
$$
k=\frac{dy}{dx}
$$
所以
$$
p_i=2x_0dy-2y_idx+2dy+(2b-1)dx
$$
当i=0时,得到迭代起点:
$$
p_0=2dy-dx
$$
当 $p_i>0时$
$$
p_{i+1}=pi+2dy-2dx
$$
当 $p_i<=0时$
$$
p_{i+1}=p_i+2dy
$$
推导到此结束,下面是实现,这个实现和TMP十分相似,但是计算量比TMP稍微小一点。
1 | |
同样的,你可以在这里找到完整代码:
BRESENHAM算法完整代码
1 | |
代码汇总
DrawLine.hpp代码
//DrawLine.hpp
#pragma once
#include <cmath>
#include <gl/glut.h>
/*
数值微分算法实现
*/
/// <summary>
/// digitial differential analyzer
/// called DAA
/// </summary>
/// <param name="startx">起始位置x</param>
/// <param name="starty"></param>
/// <param name="endx">终止位置x</param>
/// <param name="endy"></param>
void DDA_Line(int startx, int starty, int endx, int endy) {
glBegin(GL_POINTS);
if (startx != endx && starty != endy)
{
double x, y;
double k; //斜率
k = (static_cast<float>(endy - starty) /static_cast<float>(endx - startx));
x = (double)startx, y = (double)starty;
if (abs(k)<1.0) {
for (int i = 0; i < abs(endx - startx); i++) {
if (endx > startx) {
x += 1;
y += k;
}
else {
x -= 1;
y -= k;
}
glVertex2i(static_cast<int>(x), static_cast<int>(y+0.5)); //y四舍五入
}
}
else if (abs(k) > 1.0) {
for (int i = 0; i < abs(endy - starty); i++) {
if (endy > starty) {
y += 1;
x += 1.0/k;
}
else {
y -= 1;
x -= 1.0/k;
}
glVertex2i(static_cast<int>(x + 0.5), static_cast<int>(y)); //x四舍五入
}
}
}
else if (startx == endx) {//垂直画线
if (starty < endy) {
for (int i = starty; i < endy; i++) {
glVertex2i(startx, i);
}
}
else if (starty > endy) {
for (int i = endy; i < starty; i++) {
glVertex2i(startx, i);
}
}
}
else if (starty == endy) {//水平画线
if (startx < endx) {
for (int i = startx; i < endx; i++) {
glVertex2i(i, starty);
}
}
else if (startx > endx) {
for (int i = endx; i < startx; i++) {
glVertex2i(i, starty);
}
}
}
glFlush();
glEnd();
}
/*
中点画线算法实现
*/
/// <summary>
/// The Middle Point
/// Called TMP
/// </summary>
/// <param name="startx">起始位置x</param>
/// <param name="starty"></param>
/// <param name="endx">终止位置x</param>
/// <param name="endy"></param>
void TMP_Line(int startx, int starty, int endx, int endy) {
glBegin(GL_POINTS);
if (startx != endx && starty != endy)
{
bool kFlag = 0; //斜率是否大于1
int sFlag = 1; //斜率的正负
if (startx > endx) { //因为算法是x递增的,所以要保持起点x在终点左边
int tempx = startx, tempy = starty;
startx = endx, starty = endy;
endx = tempx, endy = tempy;
}
if (abs(starty - endy) > abs(startx - endx)) {
kFlag = true;
}
if (starty > endy) { //标记斜率小于零
sFlag = -1;
}
int a, b, TA, TAB, d, x, y;
if (sFlag == -1)
endy = starty + (starty - endy);
a = starty - endy;
b = endx - startx;
TA = 2 * a; //twoA
TAB = 2 * (a + b); //twoAB
d = 2 * a + b;
x = startx, y = starty;
if (!kFlag) {
for (int i = 0; i < (endx - startx); i++) {
if (d >= 0) {
glVertex2i(++x, y);
d += TA;
}
else {
glVertex2i(++x , y +=sFlag);
d += TAB;
}
}
}
else if (kFlag) {
if (kFlag == 1) {
TA = 2 * b;
d = 2 * b + a;
}
for (int i = 0; i < abs(endy - starty); i++) {
if (d >= 0) {
glVertex2i(++x , y +=sFlag);
d += TAB;
}
else {
glVertex2i(x, y+=sFlag);
d += TA;
}
}
}
}
else if (startx == endx) {//垂直画线
if (starty < endy) {
for (int i = starty; i < endy; i++) {
glVertex2i(startx, i);
}
}
else if (starty > endy) {
for (int i = endy; i < starty; i++) {
glVertex2i(startx, i);
}
}
}
else if (starty == endy) {//水平画线
if (startx < endx) {
for (int i = startx; i < endx; i++) {
glVertex2i(i, starty);
}
}
else if (startx > endx) {
for (int i = endx; i < startx; i++) {
glVertex2i(i, starty);
}
}
}
glFlush();
glEnd();
}
/*
Bresenham算法
这是图形学中用的最多的直线生成算法,全部是整数计算,加快了计算的速度
*/
/// <summary>
/// Bresenham
/// </summary>
/// <param name="startx"></param>
/// <param name="starty"></param>
/// <param name="endx"></param>
/// <param name="endy"></param>
void BRESENHAM_Line(int startx, int starty, int endx, int endy) {
glBegin(GL_POINTS);
if (startx != endx && starty != endy) {
bool kFlag = 0; //斜率是否大于1
int sFlag = 1; //斜率的正负
if (startx > endx) { //因为算法是x递增的,所以要保持起点x在终点左边
int tempx = startx, tempy = starty;
startx = endx, starty = endy;
endx = tempx, endy = tempy;
}
if (abs(starty - endy) > abs(startx - endx)) {
kFlag = true;
}
if (starty > endy) { //标记斜率小于零
sFlag = -1;
}
int x, y;
int dx, dy, p;
if (sFlag == -1)
endy = starty + (starty - endy);
dx = endx - startx;
dy = endy - starty;
x = startx, y = starty;
if (!kFlag) {
p = 2 * dy - dx;
for (int i = 0; i < (endx - startx); i++) {
if (p <= 0) {
glVertex2i(++x, y);
p += 2 * dy;
}
else {
glVertex2i(++x, y += sFlag);
p += 2 * dy - 2 * dx;
}
}
}
else {
p = 2 * dx - dy;
for (int i = 0;i < (endy - starty); i++) {
if (p <= 0) {
glVertex2i(x, y += sFlag);
p += 2 * dx;
}
else {
glVertex2i(++x, y += sFlag);
p += 2 * dx - 2 * dy;
}
}
}
}
else if (startx == endx) {//垂直画线
if (starty < endy) {
for (int i = starty; i < endy; i++) {
glVertex2i(startx, i);
}
}
else if (starty > endy) {
for (int i = endy; i < starty; i++) {
glVertex2i(startx, i);
}
}
}
else if (starty == endy) {//水平画线
if (startx < endx) {
for (int i = startx; i < endx; i++) {
glVertex2i(i, starty);
}
}
else if (startx > endx) {
for (int i = endx; i < startx; i++) {
glVertex2i(i, starty);
}
}
}
glFlush();
glEnd();
}
``` 用于测试的一个主函数
```cpp
/*
你可以使用左键绘制顶点
你可以使用右键删除顶点
直线的绘制沿着顶点顺序
*/
#include <gl/glut.h>
#include <iostream>
#include <list>
#include "DrawLine.hpp"
using namespace std;
#define m_POINT_SIZE 10
#define m_LINE_SIZE 2
list<pair<int, int >>Vertex;
void onDisplay();
void onReshape(int w, int h);
void onMouse(int button, int state, int x, int y);
void onReshape(int w, int h)
{
// 设置视口大小
glViewport(0, 0, w, h);
// 切换矩阵模式为投影矩阵
glMatrixMode(GL_PROJECTION);
// 载入单位矩阵
glLoadIdentity();
// 进行二维平行投影
gluOrtho2D(0, w, h, 0);
// 切换矩阵模式为模型矩阵
glMatrixMode(GL_MODELVIEW);
// 发送重绘
glutPostRedisplay();
}
void onMouse(int button, int state, int x, int y){
if (state == GLUT_DOWN) {
if (button == GLUT_LEFT_BUTTON)Vertex.push_back(make_pair(x, y));
else if (button == GLUT_RIGHT_BUTTON) {
auto ibeg = Vertex.begin();
while (ibeg != Vertex.end()) {
if (((x - ibeg->first) * (x - ibeg->first)) + ((y - ibeg->second) * (y - ibeg->second)) < 400) {
Vertex.erase(ibeg);
break;
}
ibeg++;
}
}
}
onDisplay();
}
void onDisplay() {
glClearColor(224 / 255.0, 237 / 255.0, 253 / 255.0,1.0);
glClear(GL_COLOR_BUFFER_BIT);
glColor3f(1.0f, 0, 0);
auto ibeg = Vertex.begin(),jbeg=ibeg;
bool flag = false;
while (ibeg != Vertex.end()) {
glPointSize(m_POINT_SIZE);
glBegin(GL_POINTS);
glVertex2i(ibeg->first, ibeg->second);
glEnd();
glPointSize(m_LINE_SIZE);
if (!flag)
flag = true;
else {
//这里可以选择直线绘制方式
BRESENHAM_Line(ibeg->first, ibeg->second, jbeg->first, jbeg->second);
//TMP_Line(ibeg->first, ibeg->second, jbeg->first, jbeg->second);
//DDA_Line(ibeg->first, ibeg->second, jbeg->first, jbeg->second);
}
jbeg = ibeg;
ibeg++;
}
glutSwapBuffers();
}
int main(int argc, char* argv[])
{
// 初始化 glut
glutInit(&argc, argv);
// 设置 OpenGL 显示模式(双缓存, RGB 颜色模式)
glutInitDisplayMode(GLUT_DOUBLE | GLUT_RGB);
// 设置窗口初始尺寸
glutInitWindowSize(1000,800);
// 设置窗口初始位置
glutInitWindowPosition(0, 0);
// 设置窗口标题
glutCreateWindow("Terix");
glutReshapeFunc(onReshape);
glutDisplayFunc(onDisplay);
glutMouseFunc(onMouse);
// 进入 glut 事件循环
glutMainLoop();
return 0;
}
``` ## 下一篇 [下一篇->圆形的绘制](https://www.cnblogs.com/zhywyt/articles/17341756.html)