第？课——基于矩阵快速幂的递推解法

第？课——基于矩阵快速幂的递推解法
由于中间的数论部分我自己学的很差，没有办法写出清晰的博客来，所以这里跳过了数论部分的博客，来到矩阵快速幂。

递推

递推是一个非常常用的工具。比如经典的斐波那契数列：

\[f(x)= \left\{ \begin{array}{**lr**} 1 &, 0\leq x\leq 1 \\ f(x-1)+f(x-2)&, 2 \leq x \\ \end{array} \right. \]

很明显，\(f(n)\)依赖于\(f(n-1)\)和\(f(n-2)\)，所以我们需要先计算\(f(n-1)f(n-2)\)才能计算\(f(n)\)。

假设我们现在需要求f(1e9+7)，你很快发现了，这个数字非常大。所以我们要求只需要结果对\(MOD\)取模就好了，而\(MOD=1e9+7\)。问题是：我们的迭代算法是\(O(n)\)的。那如何快速的求解这样一个递推问题呢？

矩阵与递推的联系

让我们站在巨人的肩膀上来看这个递推问题的第二项以及之后：

\[\begin{pmatrix}f(n)\\? \\\end{pmatrix}= \begin{pmatrix}1&1\\?&?\\\end{pmatrix}\dot\\ \begin{pmatrix}f(n-1)\\f(n-2)\end{pmatrix} \]

数学家们把这个问题用矩阵的形式表现了出来。但是矩阵上还有一行是空的。打个比方，我们在求\(f(2)\)的时候，矩阵可以写成：

\[\begin{pmatrix}f(2)\\? \\\end{pmatrix}= \begin{pmatrix}1&1\\?&?\\\end{pmatrix}\dot\\ \begin{pmatrix}f(1)\\f(0)\end{pmatrix} \]

那如果我们需要继续计算\(f(3)\)呢？

\[\begin{pmatrix}f(3)\\? \\\end{pmatrix}= \begin{pmatrix}1&1\\?&?\\\end{pmatrix}\dot\\ \begin{pmatrix}f(2)\\f(1)\end{pmatrix} \]

我们需要知道

\[\begin{pmatrix}f(2)\\f(1)\end{pmatrix} \]

可是\(f(2)f(1)\)哪里来呢？不妨把我们的通项改写一下，在计算\(f(n)\)的同时顺带计算\(f(n-1)\)？

\[\begin{pmatrix}f(n)\\f(n-1) \\\end{pmatrix}= \begin{pmatrix}1&1\\1&0\\\end{pmatrix}\dot\\ \begin{pmatrix}f(n-1)\\f(n-2)\end{pmatrix} \]

！！wow，我们得到了一个强大的新递推式子。这时候有人要不乐意了，这不是复杂化了么，我们本来只要两个数加一加，现在还要算一个2$\times$4的矩阵乘法？可是，我们的矩阵是常数。 再稍微改写一下这个式子：

\[\begin{pmatrix}f(n)\\f(n-1) \\\end{pmatrix}= \begin{pmatrix}1&1\\1&0\\\end{pmatrix}^{n-1} \\ \dot\\ \begin{pmatrix}f(1)\\f(0)\end{pmatrix} \]

相信你看到这里已经顿悟了，因为这个矩阵的高次幂我们可以大做文章！

快速幂与矩阵快速幂

快速幂

快速幂很简单，这里直接给出代码：

1
2
3
4
5
6
7
8
int quickpow(int a,int b,int x) {
	while(x>0) {
		if(x&1) a=a*b;
		b=b*b;
		x>>=1;
	}
	return a;
}

快速幂原理给一个友情链接：
快速幂总结

矩阵乘法

先放一个市面上常见的通用矩乘：

1
2
3
4
5
6
7
8
for(int i=1; i<=n; i++) {
	for(int j=1; j<=n; j++) {
		for(int k=1; k<=n; k++) {
			tmp.mat[i][j]+=(a.mat[i][k]%mod*b.mat[k][j]%mod)%mod;	\\拖慢速度
			tmp.mat[i][j]%=mod;
		}
	}
}

这个矩阵乘非常符合人的想法，但是有一个点让它比较慢，我们矩阵快速幂只需要进行幂次乘法，可以做一些优化：

1
2
3
4
5
6
7
8
for(int i=1; i<=n; i++) {
	for(int j=1; j<=n; j++) {
		for(int k=1; k<=n; k++) {
			tmp.mat[i][k]+=(a.mat[i][j]%mod*b.mat[j][k]%mod)%mod;
			tmp.mat[i][k]%=mod;
		}
	}
}

看出不一样的地方了吗？唯一的区别就在下标处。把k放在第一维会大大增加寻址的计算量，所以需要把k放在第二维上就能减少非常多的计算量。其实矩阵小的时候也没什么区别

矩阵快速幂

其实和普通快速幂没有多大区别，只需要重载一个乘法运算符就好了。这里给一份结构体加快速幂的代码：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
#include <iostream>
#include <string.h>
using namespace std;
const int mod = (int)1e9+7;
struct MyMat{
    MyMat(int n_=24,int m_=24):n(n_),m(m_){
        memset(mat,0,sizeof(mat));
    }
    int mat[25][25];
    int m,n;
    friend MyMat operator*(const MyMat&a,const MyMat&b){
        MyMat tmp;
        if(a.m!=b.n)throw("Matrix size mismatch");
        for(int i=1; i<=a.n; i++) {
            for(int j=1; j<=b.m; j++) {
                for(int k=1; k<=a.m; k++) {
                    tmp.mat[i][j]+=(a.mat[i][k]%mod*b.mat[k][j]%mod)%mod;
                    tmp.mat[i][j]%=mod;
                }
            }
        }
        tmp.n = a.n,tmp.m=b.m;
        return tmp;
    }
    friend istream& operator>>(istream&is,MyMat& M){
        for(int i=1;i<=M.n;i++){
            for(int j=1;j<=M.m;j++){
                is>>M.mat[i][j];
            }
        }
        return is;
    }
    friend ostream& operator<<(ostream&os,const MyMat& M){
        for(int i=1;i<=M.n;i++){
            for(int j=1;j<=M.m;j++){
                if(j!=1)os<<" ";
                os<<M.mat[i][j];
            }
            os<<"\n";
        }
        return os;
    }
};
MyMat quickpow(MyMat a,MyMat b,int x) {
	while(x>0) {
		if(x&1) a=b*a;
		b=b*b;
		x>>=1;
	}
	return a;
}
int main(){
    MyMat a(2,3),b(3,2);
    cin>>a>>b;
    auto ans = a*b;
    cout<<"a:\n"<<a<<"*\nb:\n"<<b<<"=\n"<<ans;
    ans = quickpow(a,ans,5);
    cout<<"a*ans^5=\n"<<ans;
}

感兴趣的可以当一个参考。下面是本地运行测试输出

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
g++ -o test test.cpp
./test
1 2 1 2 1 2 
1 2 3 1 2 3
a:
1 2 1
2 1 2
*
b:
1 2
3 1
2 3
=
9 7
9 11
a*ans^5=
2480048 2480080 2480048
3188656 3188624 3188656

解题

斐波那契数列

让我们回到经典的斐波那契数列，写出这个矩阵递推式后，加上矩阵快速幂

\[\begin{pmatrix}f(n)\\f(n-1) \\\end{pmatrix}= \begin{pmatrix}1&1\\1&0\\\end{pmatrix}^{n-1} \\ \dot\\ \begin{pmatrix}f(1)\\f(0)\end{pmatrix} \]

我们就能快速地写出斐波那契数列的代码了，和上面不同的地方只有quickpow函数的x改为了long long：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
MyMat quickpow(MyMat a,MyMat b,long long x) {
	while(x>0) {
		if(x&1) a=b*a;
		b=b*b;
		x>>=1;
	}
	return a;
}
int main(){
    long long n;
    cin>>n;
    if(n<2)cout<<"1"<<endl;
    else {
        MyMat A(2,2);
        A.mat[1][1]=1;
        A.mat[1][2]=1;
        A.mat[2][1]=1;
        MyMat x(2,1);
        x.mat[1][1]=1;
        x.mat[2][1]=1;
        auto ans = quickpow(x,A,n);
        cout<<ans.mat[1][1]<<endl;
    }
    return 0;
}

A Simple Math Problem

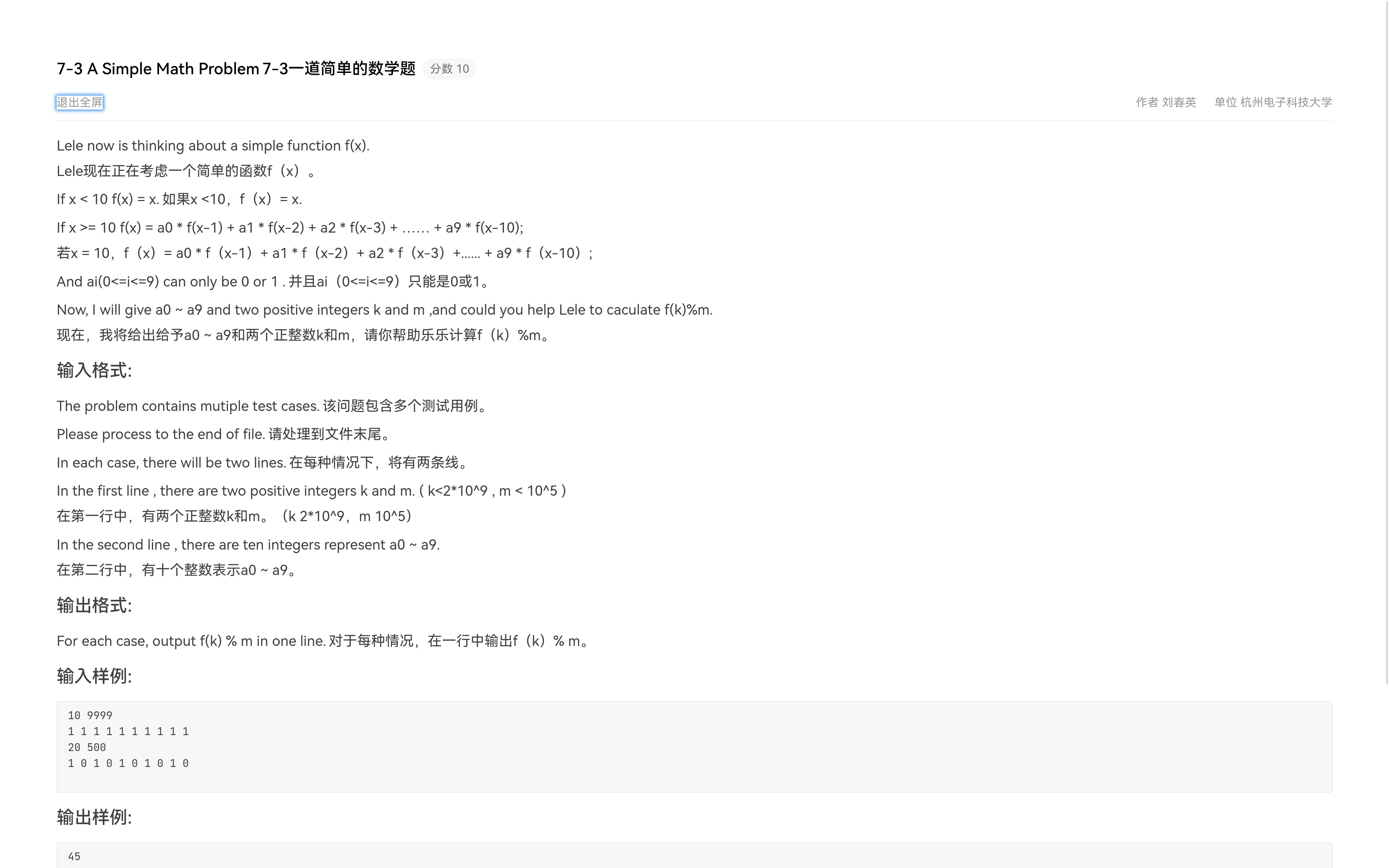
image
重点：
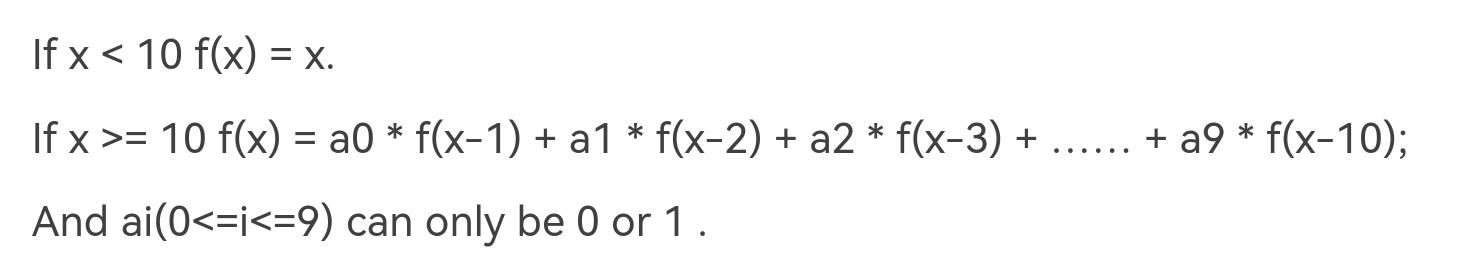
image
这个矩阵我就不写了，自己动手尝试一下吧～

Count

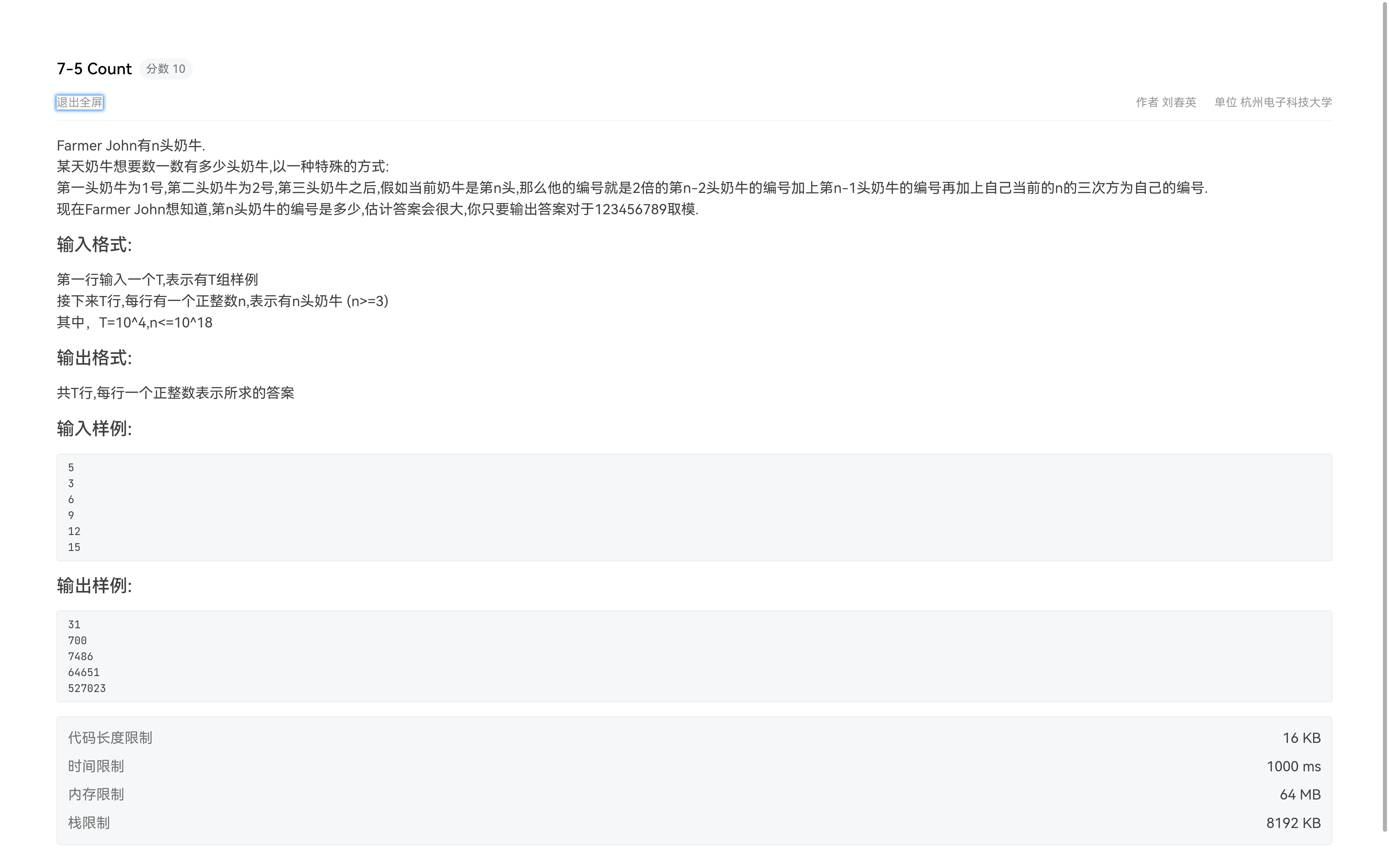
image
重点：
image

\[\left\{ \begin{array}{**lr**} f(n) = f(n-1)+2f(n-2)+n^3 \\n^3 = (n-1)^3-3n^3-3n-1\\n^2 = (n-1)^2+2n-1\\n = n-1 \end{array} \right. \]

\[\begin{pmatrix}f(n)\\ f(n-1) \\ n^3\\ n^2\\ n\\\ 1 \end{pmatrix}= \begin{pmatrix}1&2&1&3&3&1\\1&0&0&0&0&0\\0&0&1&3&3&1\\0&0&0&1&2&1\\0&0&0&0&1&1\\0&0&0&0&0&1 \end{pmatrix}\\ \dot\\ \begin{pmatrix}f(n-1)\\f(n-2)\\(n-1)^3\\(n-1)^2\\n-1\\1\end{pmatrix} \]

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
//AC代码
#include <iostream>
#include <string>
#include <sstream>
#include <string.h>
using namespace std;
const int mod = (int)123456789;
struct MyMat{
    MyMat(int n_=24,int m_=24):n(n_),m(m_){
        memset(mat,0,sizeof(mat));
    }
    int mat[25][25];
    int m,n;
    friend MyMat operator*(const MyMat&a,const MyMat&b){
        MyMat tmp;
        if(a.m!=b.n)throw("Matrix size mismatch");
        for(int i=1; i<=a.n; i++) {
            for(int j=1; j<=b.m; j++) {
                for(int k=1; k<=a.m; k++) {
                    tmp.mat[i][j]+=1ll*a.mat[i][k]*b.mat[k][j]%mod;		//1ll防止爆int
                    tmp.mat[i][j]%=mod;
                }
            }
        }
        tmp.n = a.n,tmp.m=b.m;
        return tmp;
    }
    friend istream& operator>>(istream&is,MyMat& M){
        for(int i=1;i<=M.n;i++){
            for(int j=1;j<=M.m;j++){
                is>>M.mat[i][j];
            }
        }
        return is;
    }
    friend ostream& operator<<(ostream&os,const MyMat& M){
        for(int i=1;i<=M.n;i++){
            for(int j=1;j<=M.m;j++){
                if(j!=1)os<<" ";
                os<<M.mat[i][j];
            }
            os<<"\n";
        }
        return os;
    }

};
MyMat quickpow(MyMat a,MyMat b,long long x) {
	while(x>0) {
		if(x&1) a=b*a;
		b=b*b;
		x>>=1;
	}
	return a;
}
int main(){
    std::string instr("1 2 1 3 3 1  1 0 0 0 0 0  0 0 1 3 3 1  0 0 0 1 2 1  0 0 0 0 1 1  0 0 0 0 0 1  2 1 8 4 2 1");
    std::stringstream is;
    is<<instr;
    MyMat A(6,6);
    MyMat x(6,1);
    is>>A>>x;
    long long n;
    cin>>n;
    for(int i=0;i<n;i++){
        long long m;
        cin>>m;
        if(m<=2)cout<<m<<endl;
        else {
            auto ans = quickpow(x,A,m-2);
            cout<<(ans.mat[1][1])%mod<<endl;
        }
    }
    return 0;
}

END

第？课——基于矩阵快速幂的递推解法
http://hexo.zhywyt.me/posts/62236/
作者
zhywyt
发布于
2024年5月4日
更新于
2024年10月22日
许可协议