games101 HomeWork1
games101 HomeWork 1
说起来我自己写games101的作业也是曲曲折折,虚拟机很卡就拿VS配环境,Windows不会配环境,就装Linux,现在装上了Linux,却因为没有经验把Windows格式化了(我是真的沙比),好在还是开始做了,也挺顺利的,所以再来记录一下作业。
这里是作业框架的下载作业框架下载
导航
基础部分
这里需要完成两个函数,一个是模型变换矩阵,一个是透视投影矩阵。
模型变换矩阵
逐个元素地构建模型变换矩阵并返回该矩阵。在此函数中,你只需要实现三维中绕 z 轴旋转的变换矩阵,而不用处理平移与缩放。
这个部分的实现非常简单,只需要记住这个公式就好了。这里给出绕三个轴旋转的旋转矩阵:
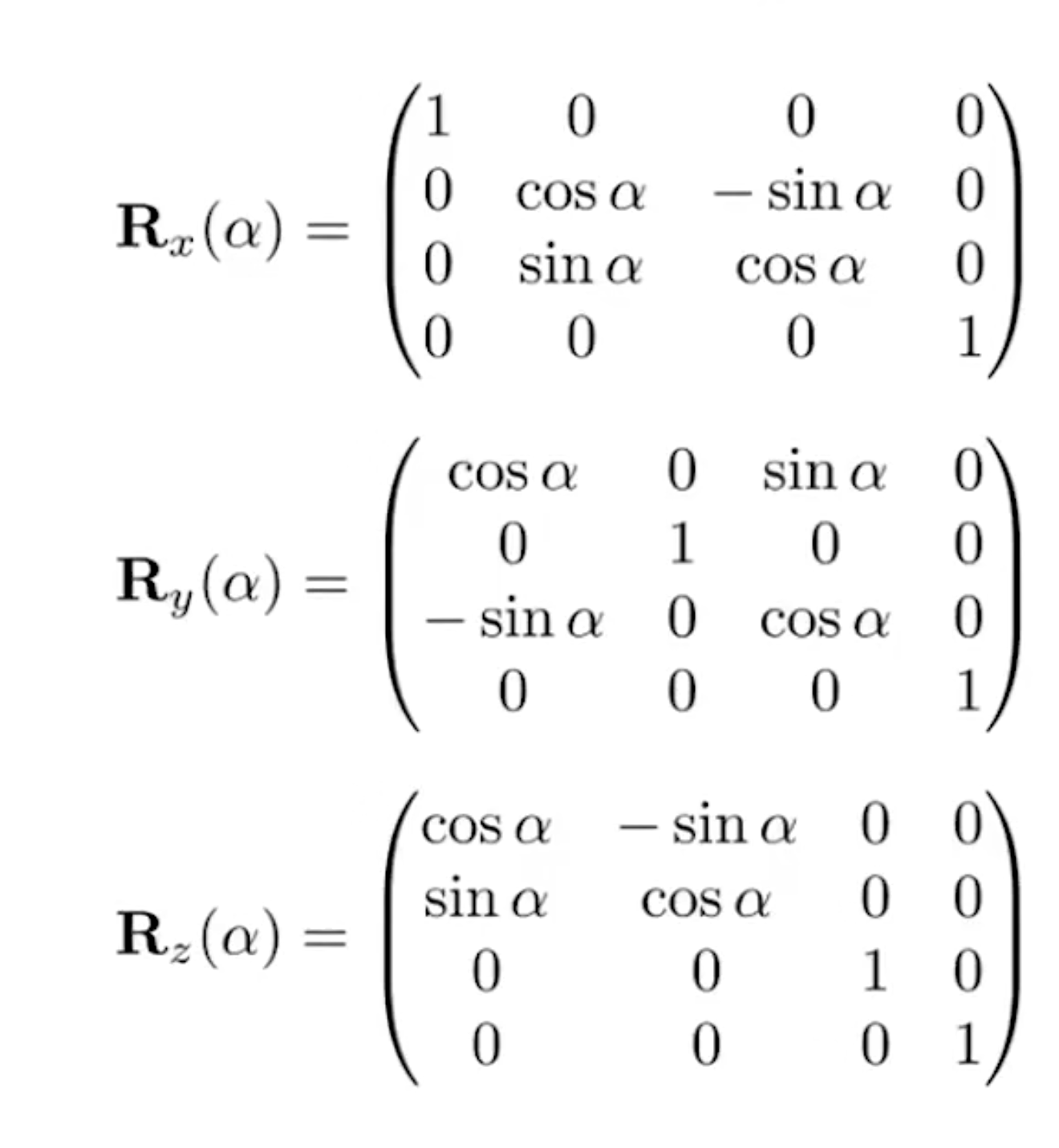
代码实现:
1 | |
透视投影矩阵
使用给定的参数逐个元素地构建透视投影矩阵并返回
该矩阵。
这个题目的参数定义其实不是很明显(至少位蒙b了很久),先看一下函数原型:
1 | |
来解读一下前两个参数,eye_fov指的是摄像机的垂直可视角度,aspect_ratio指的是摄像机的长宽比。使用这四个值也能算出正交投影矩阵。(下图只供参考)
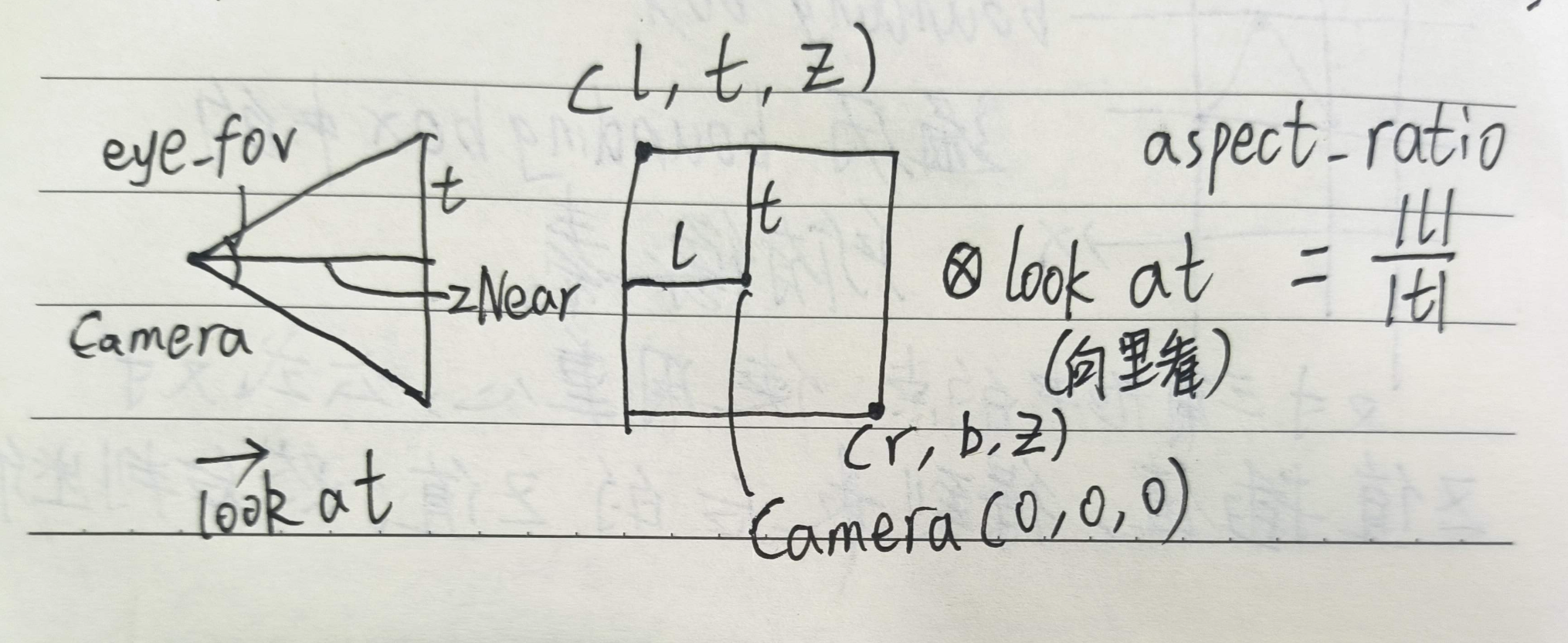
我们从透视投影矩阵开始:
根据课堂上的推导,我们已经知道透视投影矩阵的最终结果,并且所需要的值只有zNear和zFar,于是我们能直接写出这个矩阵:
1 | |
然后是我们的正交投影部分了,正交投影需要用到的数据有六个,分别是长方体的参数。
$$[l,r]\times[b,t]\times[f,n]$$
先把正的数据处理掉,直接给出答案,再证明
- \(t=zNear*tan(eye\_fov/2)\)(弧度化后)
- \(r=t*aspect\_ratio\)
另外的l和b分别等于r和t的相反数。
证明如下:(仅供参考)
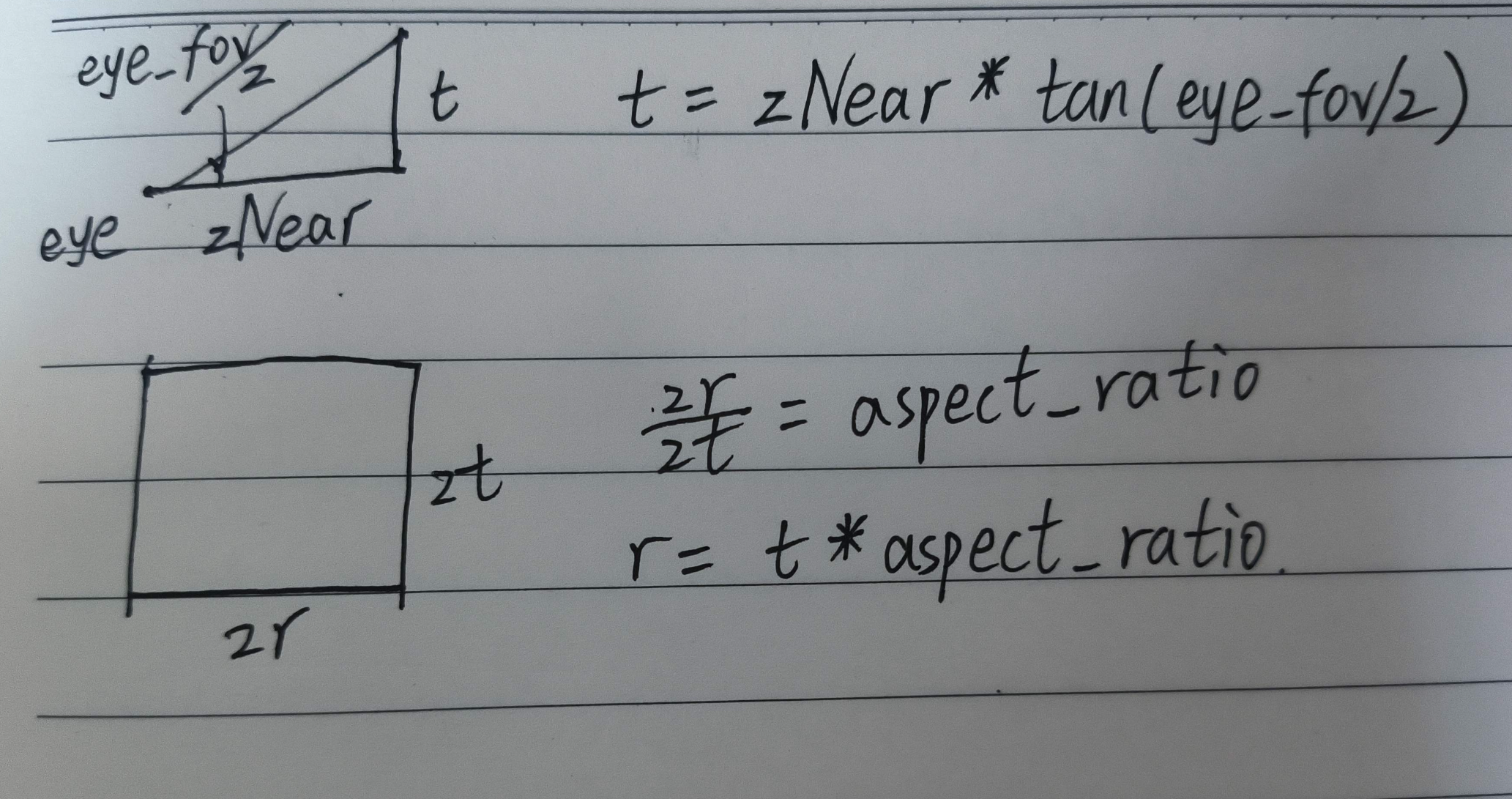
最后还剩下n和f,这两个数和他们的名字差别很大,分别是后和前,赋值的时候需要小心,而且他们的值并不是zNear和zFar分别赋值,而是相反数赋值。如下
1 | |
有了数据,我们就可进行投影矩阵的实现了,正交投影矩阵如下:
1 | |
普通要求代码汇总
1 | |
提升部分
提升部分要求:在 main.cpp 中构造一个函数,该函数的作用是得到绕任意
过原点的轴的旋转变换矩阵。根据101中的推导,我们需要计算的东西并不多,按要求写好就行了。我选择重载get_model_matrix函数,来实现任意旋转轴的旋转操作。
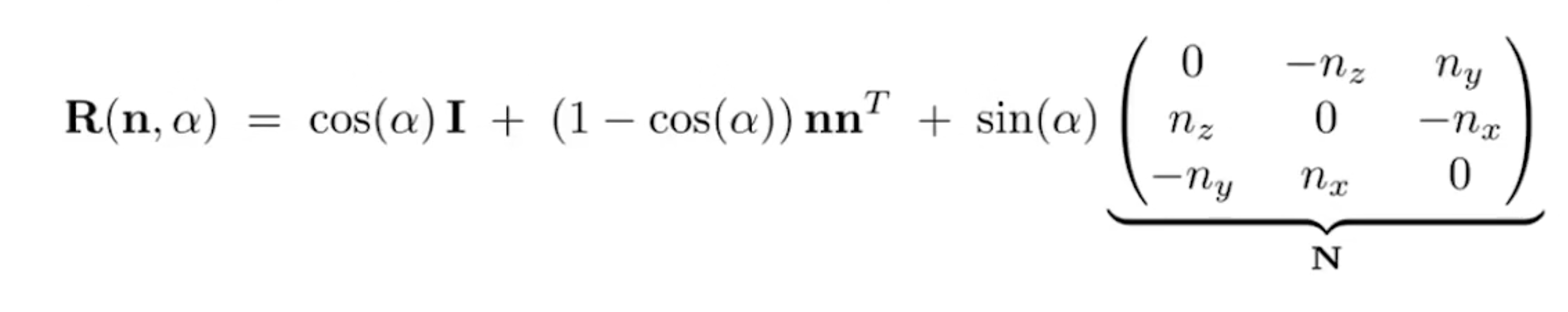
1 | |
其余代码和普通要求一致。得到结果如下:
结果
因为是第一次作业,所以我这里给出编译的操作:
先来到作业目录

创建build文件夹
来到build文件夹
使用上级目录创建项目文件
构建编译,这里的-j8是表示调用的核心数量,最后一句target Rasterizer表示可执行文件为Rasterizer
运行

按下Esc或者Ctrl+C停止
全部指令汇总
1 | |
普通要求
运行指令与结果
./Rasterizer 不带参数运行

./Rasterizer -r 0 output.png无旋转保存图片


./Rasterizer -r 90 output90.png旋转保存图片

提升要求
先介绍一下main函数的两个参数argc和argv
argc全称arugment count,表示调用程序的时候,传入的参数的个数。argv全称argument vector,表示调用程序的时候,传入的参数向量,类型为字符串
默认的,argv[0]是调用程序的完整路径,然后argv[0]-argv[argc-1]都是可以访问的字符串。在程序中,我们可以使用标准库定义的stof函数,把字符串转成浮点型,或者使用stod把字符串转化成整形。知道这一点之后,我们就可以设计一个main函数来把我们自定义的旋转轴作为参数传入程序了。
这里是我自己设计的一个传参方案,有兴趣的可以读一下程序。
main.cpp
1 | |
部分效果如下:
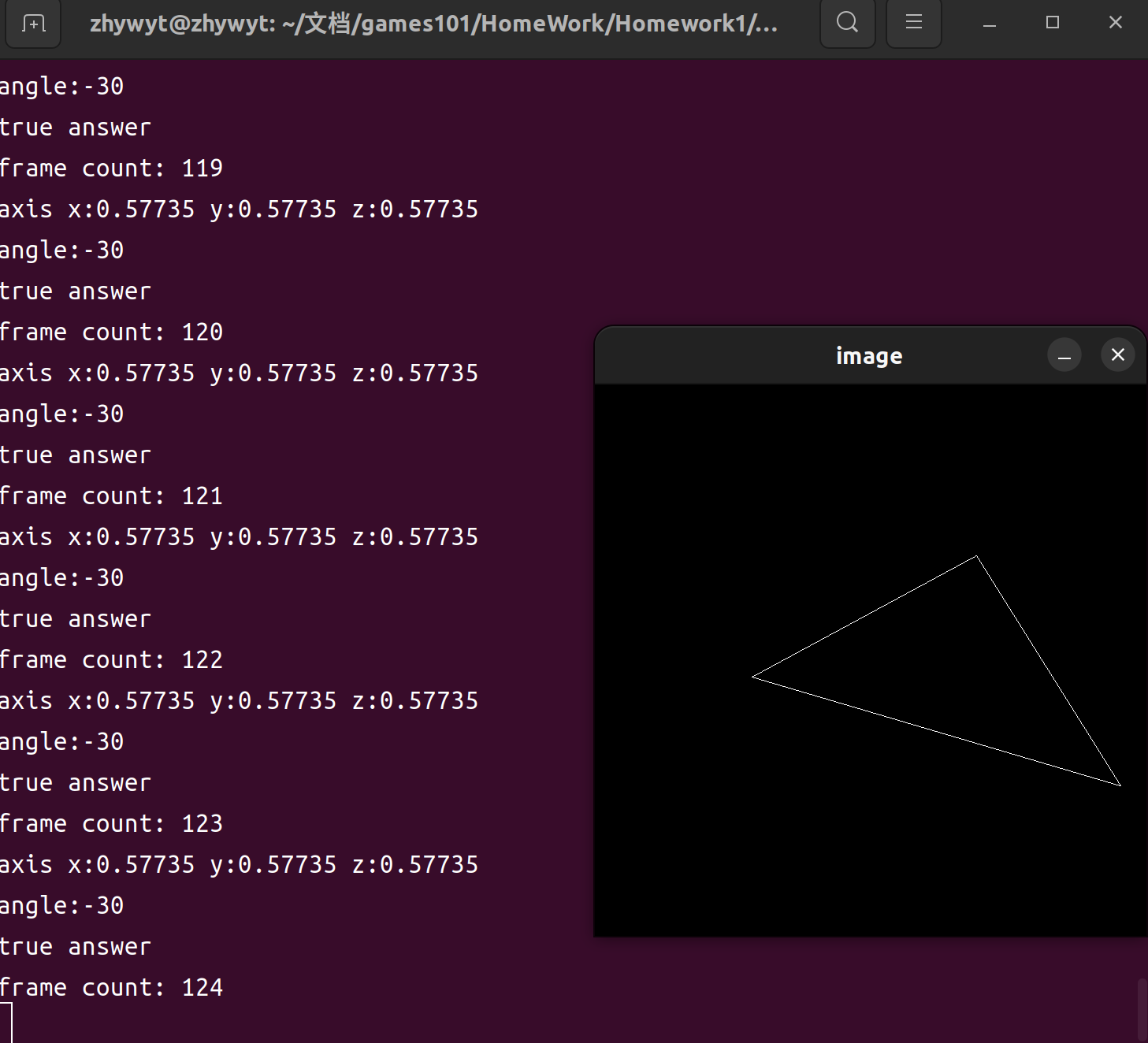
可执行操作如下
./Rasterizer -p使用便阅读版本矩阵进行计算./Rasterizer -m使用简便版本矩阵进行计算
games101 Hw1 到此就结束啦!
2023.8.17
写完之后,感觉少了点什么,于是便有了下面的东西。
框架解读
作业一的文件如下
- main.cpp
- rasterizer.cpp
- rasterizer.hpp
- Triangle.cpp
- Triangle.hpp
读框架代码要从接口开始,也就是头文件,我们先注意一下各个头文件的引用情况:
1 | |
可以看到,Triangle.hpp是一个独立的类,只需要依赖数学库Eigen,我们从这个三角形类开始。
Triangle
数据成员
这里用到的三角形类存储了一个三角形的顶点部分信息,以达到绘制一个线框所需要的数据结构。具体有这些:
Vector3f v[3];顶点坐标Vector3f color[3];顶点颜色Vector2f tex_coords[3];纹理坐标Vector3f normal[3];法线方向
其中只有顶点坐标在作业一中用到了。
接口函数
1 | |
函数实现
只有一个函数是值的讲解的toVector4:这个函数把三角形顶点坐标转化为齐次坐标后返回。
std::transform是一个通用算法,用于对输入范围中的元素执行给定的操作,并将结果存储在输出范围中。在这个例子中,我们使用std::transform(std::begin(v), std::end(v), res.begin(), [](auto& vec) { ... })来将v数组中的每个Vector4f对象转换为res数组中的对应对象。[](auto& vec) { ... }是一个lambda表达式,用于定义转换操作。
1 | |
rasterizer
这个类就很有意思了,从类的数据成员开始看:
1 | |
frame_buf存储的是最后的颜色结果,虽然直译是指框架缓存。(英语不好,勿喷)
有了这些数据成员,就开开始写数据的构造和赋值了。构造只有对显示区域参数的初始化:
构造
1 | |
赋值
需要外部输入的数据成员还有
- model
- view
- projection
- pos_buf
- ind_buf
1 | |
上面三个MVP函数是非常简单的,没什么好讲的,但是导入顶点坐标和索引的函数,可得好好讲讲。
首先是为什么这个两个函数返回值分别是rst::pos_buf_id和rst::ind_buf_id ,在原代码框架里给了这么一段解释:
1 | |
在我们的draw函数里面,直接对id进行了下标访问,因为我们不希望再去浪费查找的时间,这样一个设计可以让程序高效而安全。这就像是给一个整形变量贴上了标签一样。两个不同的返回值类型的存在,使得我们可以存在相同的id在pos_buf和ind_buf中,而不会产生问题。
而至于为什么要返回这么一个值呢?
这是因为我们在使用rasterizer类的时候,需要获得导入数据的控制buf_id,才能对导入的数据进行访问。
输出
数据成员的初始化和赋值都已经解决了,接下来就是如何准确的进行光栅化的问题了。光栅化要做的事情就两件,一、把颜色缓存填充好;二、深度缓存填充好。
一、颜色缓存
首先实现一个填充颜色的小函数rst::rasterizer::set_pixel(const Eigen::Vector3f& point, const Eigen::Vector3f& color)
作为rst::rasterizer 类的成员函数,他需要设置指定点的颜色,但是注意frame_buf是一个数组,数组意味着越界的风险,所以需要在设置之前判断下标的位置。
1 | |
二、深度缓存
这个作业没有涉及到深度缓存,因为绘制的是一个平面的三角形,所以深度缓存留到下一次作业讲解。